impossible figure

Impossible trident.

An impossible figure is an image in two dimensions of an object that, because of spatial inconsistencies, is impossible to realize fully in three dimensions. Among the best known impossible figures are the Freemish crate, the impossible trident, the Penrose stairway, and the Penrose triangle, all of which are described below. Notable pioneers of this peculiar form of representation have been Oscar Reutersvärd, Roger Penrose (and his father), and M. C. Escher.

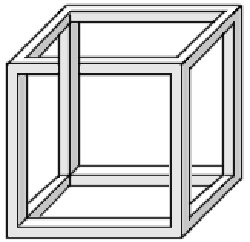
Freemish crate

The Freemish crate is an impossible figure that can be drawn but not built. Also called Escher's cube or Hyzer's illusion, it is depicted in M. C. Escher's 1958 lithograph Belvedere and was subsequently redrawn by C. F. Cochran (1966) in the form of a crate.

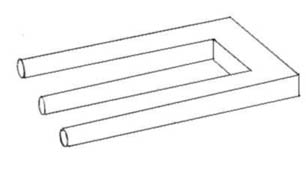
Impossible trident

The impossible trident is one of the most notorious impossible figures. It was first seen by many when it appeared on the cover of the Mar 1965 issue of Mad magazine. The two halves of the figure seem perfectly reasonable in themselves. When the top part is covered, the bottom part is taken to be three separate cylinders or tubes. With the bottom part hidden, the foreground figure is interpreted as being built of flat faces making two rectangular prongs. The trouble is that these two aspects of the figure are totally incompatible. Somewhere in the middle, the foreground and background swap places and give rise to an irreconcilable paradox.

Over the years, countless adaptations of the trident have appeared with names such as the devil's fork, the three stick clevis, the blivit, the impossible columnade, the trichotometric indicator support, and, most extravagantly, the triple encabulator tuned manifold. Swedish artist Oscar Reutersvärd's mastery of such figures has led him to draw thousands of variations on the theme. When the figure is drawn long, it is easy to perceive locally as a three-dimensional object and to overlook its inherent inconsistency, because the contradictory clues are too well separated. When the figure is of medium length, the figure is easily interpreted as a three-dimensional object, and its impossibility is quickly perceived. If the prongs are very short, the two different interpretations vie for acceptance within the same local area; thus there is no consistent interpretation and the illusion breaks down. Some early writers commented that the impossible trident couldn't be built in any form in three dimensions. However, this has been shown to be false. In 1985, the Japanese artist Shigeo Fukuda made a 3-d model of the trident in the form of classical columns in which the illusion works – from one critical angle.

The origins of the figure are uncertain. It turns out that Mad magazine bought the illustration rights from a contributor who claimed that it was original; however, the magazine's management soon found out to their embarrassment that the figure had been previously published. It began to surface in several popular engineering, aviation, and science-fiction periodicals in May and Jun of 1964. D. H. Schuster published an article that same year in the American Journal of Psychology, which first brought the figure to the attention of the psychological community.

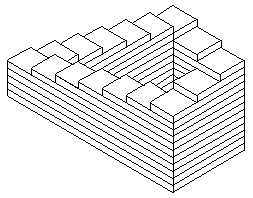
Penrose stairway

A Penrose stairway is an impossible figure named after by the British geneticist Lionel Penrose (1898-1972), father of Roger Penrose. It served as an inspiration for the staircase in M. C. Escher's famous print "Ascending and Descending." Although the Penrose stairway cannot be realized in three dimensions, this impossibility is not immediately perceived and, in fact, the paradox is not even apparent to many people at a quick glance. Although Escher and the Penroses made the Stairway famous, it was, unbeknownst to them, independently discovered and refined years before by the Swedish artist Oscar Reutersvärd. In the 1960s the Stanford psychologist Roger Shepard created an auditory analogue of the Stairway.

Penrose triangle

The Penrose triangle is the most famous and one of the simplest impossible figures. Its roots go back to 1934 when Oscar Reutersvärd made the first recognizable impossible triangle out of a strange two-dimensional representation of cubes; this artwork appeared on a Swedish postage stamp issued in 1982.

In 1954, Roger Penrose, after attending a lecture by M. C. Escher, rediscovered the impossible triangle and drew it in its most familiar form, which he published in a 1958 article in the British Journal of Psychology, coauthored with his father Lionel.¹ Penrose was also unfamiliar with the work of Reutersvärd, Piranesi, and others who had created impossible figures previously. Penrose's impossible triangle, unlike Reutersvärd's earlier version, was drawn in perspective, which added an additional size paradox to the object. In 1961, Escher, inspired by Penrose's version of the impossible triangle (he was sent a copy of the article by the Penroses), incorporated it into his famous lithograph "Waterfall."