Roger Penrose is an English mathematical physicist famous for his important contributions to cosmology and the physics of black holes, for his controversial views on the nature of human consciousness and its relationship to quantum mechanics, and for his work in the field of recreational mathematics.

 

The Penrose tiling and the Penrose triangle are named after him, but not the Penrose stairway, which is named after his father. In his book The Emperor's New Mind¹ he argues that there must be errors in the known laws of physics, notably in quantum mechanics, and that true artificial intelligence is impossible. The latter claim is based on his assertion that humans can do things outside the power of formal logic systems, such as knowing the truth of unprovable statements, or solving the halting problem (claims that were originally made by the philosopher John Lucas of Merton College, Oxford). These are controversial views with which most in the mathematical and computer science communities disagree.

 

Penrose diagram

A Penrose diagram, named after Roger Penrose, is a diagram that shows the global causal structure of a spacetime. It is a spacetime diagram in which all light rays are shown as traveling at 45° and in which, therefore, all particles with mass are shown as traveling on trajectories that lie within the light cone which sits at every point in the diagram. A Penrose diagram allows even infinite spacetime to be represent finitely by means of an appropriate change of coordinates.

 

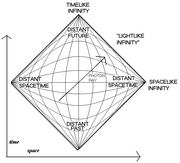Penrose diagram of the universe

 

Penrose tiling

A Penrose tiling is a kind of aperiodic tiling discovered by Roger Penrose². In 1973 he announced a tiling made from a set of six tiles and then, by slicing and re-gluing, was able to reduce the number of tiles to just two.

 

The most elegant of Penrose tilings use two rhombi, a thick one and a thin one, which are fitted together so that no two tiles are aligned to form a single parallelogram (otherwise, a single rhombus could be used to make a periodic tiling). All angles are multiples of (π/5) radians (36°, or one tenth of a circle). Each tile has four sides with a length of one unit. One tile has four corners with the angles 72°, 72°, 108°, and 108° (2, 2, 3, and 3 multiples of 36°); the other has angles of 36°, 36°, 144°, and 144° (1, 1, 4, and 4 multiples of 36°). On each tile one of the vertices (corners) is colored black and two of the sides are marked with arrows.

 

The only rules for assembling the tiles to ensure an aperiodic tiling are that two adjacent vertices must be of the same color, and two adjacent edges must have arrows pointing in the same direction or no arrows at all. These rules ensure that, taken over a large enough area of the plane, the pattern of tiles doesn't repeat. In a correct Penrose tiling, the ratio of thick rhombi to thin ones is always the same and is equal to the golden ratio.

 

Although Penrose tilings started out as nothing more than an interesting mathematical diversion, they have turned out to mimic the arrangements of atoms in some newly discovered materials, known as quasicrystals.

 

Referencs

1. Penrose Roger. The Emperor's New Mind. New York: Oxford University Press, 1989.

2. Gardner, Martin. Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix. New York: W. H. Freeman, 1989.