quadrilateral
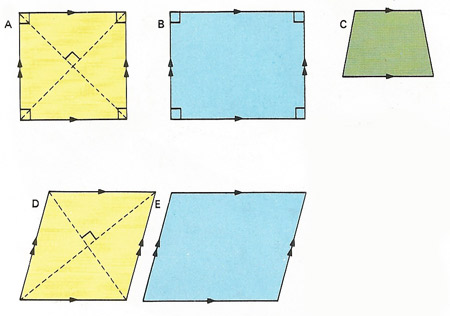
Figure 1. Quadrilaterals include a square [A] with right-angles and all its sides equal and parallel; a rectangle [B] with only opposite sides equal; a trapezium or (in the US) trapezoid [C] with only two opposite sides parallel; a rhombus [D] and a parallelogram [E], both with opposite sides parallel and no right-angles.
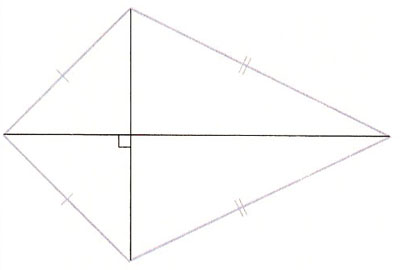
Figure 2. A kite, the diagonals of which intersect at right angles.
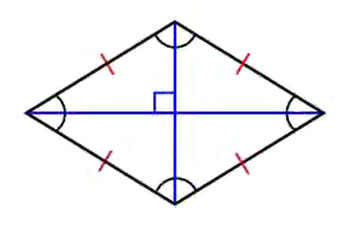
Figure 3. Rhombus.
A quadrilateral is a polygon that has four sides and four vertices (corners). Quadrilaterals, and polygons in general, may be convex or concave.
A convex quadrilateral may be further classified (Figure 1) as a trapezoid (US) or trapezium (UK and other non-US), a trapezium (US) or general irregular quadrilateral (non-US); an isosceles trapezoid (US) or an isosceles trapezium (UK) (two of the opposite sides parallel, the two other sides equal, and the two ends of each parallel side of equal angles); a parallelogram (opposite sides are parallel); a kite (two adjacent sides of equal length, the other two sides of equal length); a rhombus (four sides of equal length); a rectangle (each angle is a right angle); or a square (four sides of equal length, each angle a right angle).
Types of quadrilateral
Dart
 |
Kite
A kite (Figure 2) is a quadrilateral, with two pairs of congruent adjacent sides, that is named after one of the traditional forms of toy kite. The toy itself probably draws its name from the bird commonly called a kite, or kyte, in England. The old English form of the word, cyte, may in turn derive from an early German name for an owl.
A non-convex kite is often called a dart, a term used by Roger Penrose in his proof on a non-periodic tiling of the plane (see also Penrose tiling). Proclus referred to this shape as a "four-sided triangle" and spoke of it as a geometric paradox. John Conway has pointed out that there is no special name for a quadrilateral that has two pairs of equal sides that, unlike in the case of a kite, are not parallel sides. He proposed the name strombus for such a figure, from the Greek for a spinning top.
Parallelogram
A parallelogram is a quadrilateral whose opposite sides are parallel, and whose opposite angles, therefore, are equal.
Rectangle
A rectangle is a quadrilateral whose interior angles are all 90°. If all of its sides are the same length, it is a square. A rectangle is a special case of a parallelogram.
An oblong is alternate name for any rectangle that is not a square. The word comes from the Latin ob ("excessive") and longus ("long"). See also oblong number.
The smallest square that can be cut into m × n rectangles, such that all m and n are different integers, is the 11 × 11 square, and the tiling uses five rectangles. The smallest rectangle that can be cut into m × n rectangles, such that all m and n are different integers, is the 9 × 13 rectangle, and this tiling also uses five rectangles.
Rhombus
A rhombus (Figure 3) is a quadrilateral in which both pairs of opposite sides are parallel and all sides are the same length, that is, an equilateral parallelogram. A rhombus is also sometimes called a rhomb or a diamond. A rhombus whose acute angles are 45° is called a lozenge.
The diagonals p and q of a rhombus are perpendicular and satisfy the relationship p 2 + q 2 = 4a 2. The area of a rhombus is given by A = ½ pq.
Square
A square is a quadrilateral with four equal sides that meet at right angles.
Trapezoid and trapezium
These terms mean different things in the US and outside the US. In the US, a trapezoid is a quadrilateral with one pair of parallel sides, which in Britain and elsewhere is known as a trapezium. The American definition of a trapezium is a quadrilateral with no parallel sides; elsewhere such a shape is known as a general irregular quadrilateral. An isosceles trapezoid (US) or an isosceles trapezium (elswhere) has two of the opposite sides parallel, the two other sides equal, and the two ends of each parallel side of equal angles.
If the parallel sides are of length a and b, and h is the perpendicular distance between them, then the area of the trapezoid is given by A = ½ (a + b)h.
Three-dimensional shapes with quadrilateral bases
Quadrangular prisms and quadrangular pyramids are ones whose bases are quadrilateral.
Cyclic quadrilateral
A cyclic quadrilateral is one that can be drawn inside in a circle so that all four vertices touch the circumference.
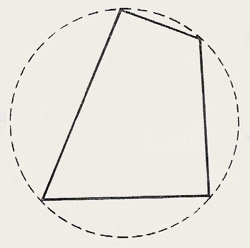 |
| Cyclic quadrilateral.
|
Aubel's theorem
Aubel's theorem states that given a quadrilateral and a square drawn on each side of it, the two lines connecting the centers of the squares on opposite sides are perpendicular and of equal length.
Ptolemy's theorem
Ptolemy's theorem states that the sum of the products of the two pairs of opposite sides of a convex cyclic quadrilateral is equal to the product of the lengths of the diagonals. It is named after the mathematician, astronomer, and geographer Ptolemy of Alexandria.


