inclined plane

An inclined plane is a practical solution to the problem of moving a heavy load up or down through a significant height. In a multi-storey car park the vehicles have to descend to street level from a great height. A long ramp – an inclined plane – would provide such a facility but it would take up a lot of room. Winding the ramp round and round, like the exit from this car park, saves space. The geometry of the ramp is like a screw thread.
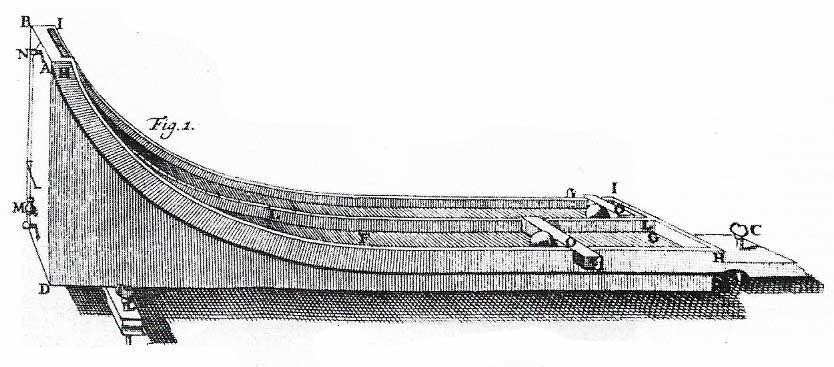
Galileo's research on the motion of balls rolling down an inclined plane led to formulae that were predecessors of Newton's three laws of motion. With his experiments Galileo in effect founded the science of dynamics. The illustration is of an 18th-century experiment in the same tradition.
The inclined plane is one of the traditional types of simple machine. Like the pulley and lever, it provides a means of raising a heavy load easily. It is particularly useful for loading barrels and drums since they can be rolled up the incline. The inclined plane was one of the few machines available in ancient times – for instance the early Egyptians used inclines on a grand scale in the construction of the pyramids.
It is easier to push a load of mass m up a slope of angle θ to the horizontal than it is to lift it vertically. The minimum force needed to push a load up an inclined plane is mg sin θ, where g is acceleration due to gravity.
If the plane is at a steep angle a greater force is needed to move the load than if the plane is only tilted slightly. However, the total work required to raise the load through the same vertical distance will be the same irrespective of the angle of inclination of the plane. But in addition work has to be done to overcome the frictional forces between the load and the plane, and these are reduced as the angle that the plane makes with the horizontal is increased.
The velocity ratio of any machine may be found by dividing the distance through which the effort moves by the vertical distance through which the load is raised. As with all other machines the velocity ratio of an inclined plane is calculated from its dimensions. The distance through which the effort moves is the distance it moves along the plane, while the distance through which the load is raised is the vertical distance through which it is lifted up.
Since frictional losses have a much greater effect on the efficiency of the inclined plane than with other machines (particularly pulleys), there is little advantage to be gained from calculating the mechanical advantage (load/effort) from theoretical consideration. Rather, the mechanical advantage may be found experimentally and used as a means of estimating the magnitude of the frictional force.
The rolling friction experienced when loading barrels (and other objects of circular cross-section) is small compared with the sliding friction which must be overcome when rectangular boxes are being pushed (or pulled) up an incline. It is for this reason that the inclined plane was used for many years for loading barrels. Over the past few decades, the extra work needed to load boxes has been considerably reduced by the introduction of inclined planes incorporating metal rollers. Here again the friction force has been reduced by changing sliding friction into rolling friction.


