inverse-square law
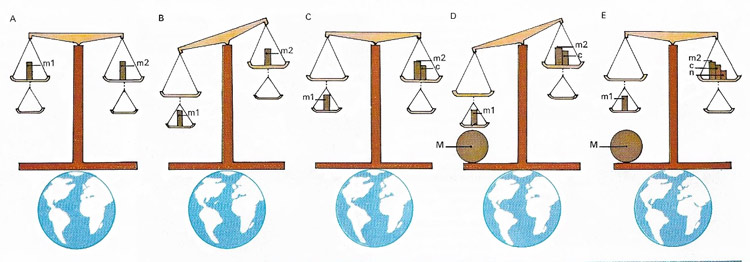
Figure 1. Earth's mass can be measured by means of a tall balance with two pans on each side.
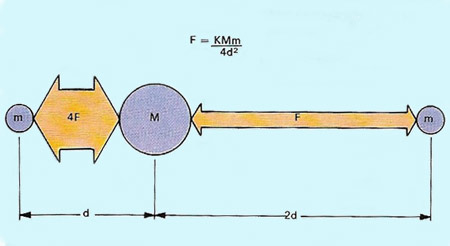
Figure 2; Inverse-square law.
Three forces demonstrate the property of action at a distance: gravity and electric and magnetic forces. These three forces obey a common law that describes how the magnitude of the force depends on the object producing it, the object affected by it, and the distance separating the two. It is called the inverse-square law. If the distance between two bodies is doubled, then the force between them falls by one-quarter, and so on.
Isaac Newton was first to realize this type of law applied to the gravitational force of attraction when performing calculations on the speed of the Moon in orbit round the Earth. His law of gravity states that the attractive force between two bodies is proportional to the product of their masses divided by the square of the distance between them. A century later, Henry Cavendish used this law to produce the first estimate of Earth's mass. He was also responsible for one of the best experimental verifications of the use of the inverse-square law to describe the force between electrostatic charges. Its use was further verified in 1870 by James Clerk Maxwell who showed that the inverse-square law was true to one part in 20,000.
Measurement of Earth's mass
Earth's mass (MEarth) can be measured by means of a tall balance with two pans on each side (see diagram above). Initially m1 balances m2 (A) but when m1 is moved to the lower pan it weighs more, being closer to the Earth (b). Mass c is used to restore the balance (c). Next the large mass M is used to make m1 weigh more, by gravitational attraction (D). Balance is restored (E) with mass n. If R is Earth's radius and d is the distance between m1 and M, then Newton's law states:
(m1 × M)/d2 = (n × MEarth)/r2
The distance of the pans on each side must be great enough to prevent M from having significant gravitational pull on the other masses.


