knot
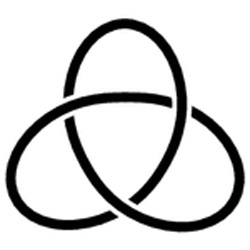
Trefoil knot.
Never cut what you can untie.
–Joseph Joubert
A knot is a closed curve in three dimensions. The two simplest nontrivial knots are the trefoil knot, whose picture has three crossings, and the figure-eight knot, whose picture has four. To date, more than 1.7 million non-equivalent knots with pictures of 16 or fewer crossings have been identified.
The mathematical theory of knots was born out of attempts to model the atom. Near the end of the 19th century, William Thomson (Lord Kelvin) suggested that different atoms were actually different knots tied in the ether that was believed to permeate all of space. Physicists and mathematicians set to work making a table of distinct knots, believing they were making a table of the elements. A pioneer in this effort, alongside Thomson, was Peter Tait. By the time the theory of the ether vanished into thin air, knot theory was firmly tied into mainstream mathematics. It blossomed with the development of topology and eventually led to important applications in DNA research and molecular biology. Today it is one of the most active areas of mathematical research.


