TOPOLOGY
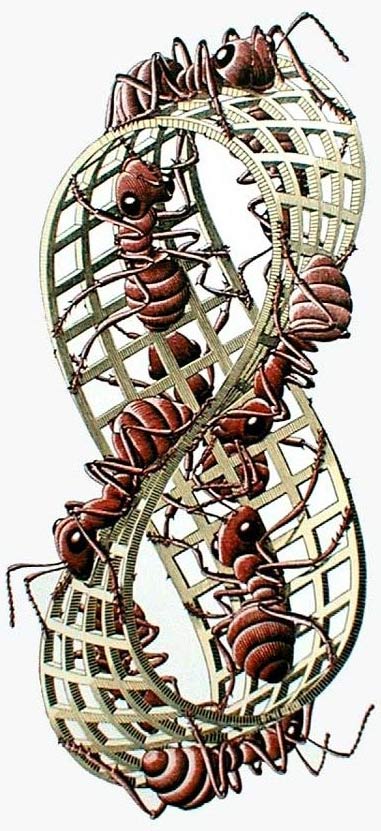
Moebius Strip II by M. C. Escher. These ants illustrate the counterintuitive properties of the Möbius band – an ordinary band with a half-twist. All are on the one side but appear to be on opposite sides. A band made with two half-twists does have two sides. The number of twists dictates the number of sides and dramatically affects the result produced by cutting along the middle. Topology allows the exploration and description of such spatial relationships..
Alexander's
Horned Sphere
algebraic
topology
Banach-Tarski
paradox
Betti
number
Borromean
rings
Borsuk-Ulam
theorem
braid
Brouwer
fixed-point theorem
bundle
Calabi-Yau
space
closed
cohomology
connected
continuity
diffeomorphism
differential
topology
dimension
disk (mathematics)
Earthshapes
Euclidean
geometry
Euler
characteristic
foliation
genus
Gordian
Knot
hairy
ball theorem
ham
sandwich theorem
Hilbert
space
homeomorphic
homology
homotopy
Klein
bottle
knot
manifold
Möbius
band
non-orientable
surface
orientable
surface
pleated
surface
Poincaré's
conjecture
point-set
topology
projective
plane
Riemann
surface
round
simply-connected
space
sphere
tie knot
topological dimension
topological
group
topological
space
topology
torus
Whitney's
umbrella


