Rayleigh criterion
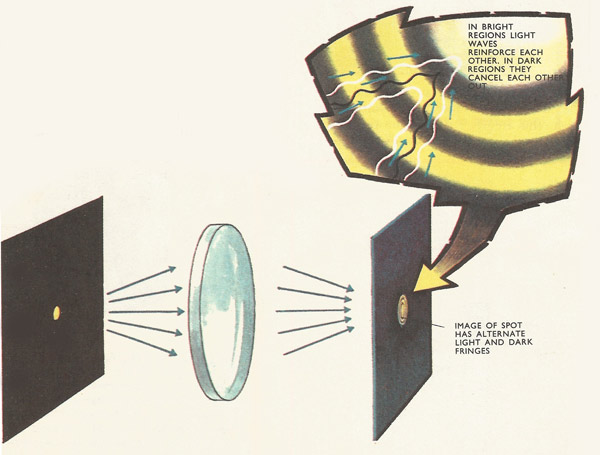
An image of a single bright spot is formed by the lens. Diffraction effects give the image a set of circular alternate light and dark rings around the central bright spot. (Inset) Light falls on each part of the image from all directions. In a bright region the light waves reinforce each other, in dark regions they cancel each other out.
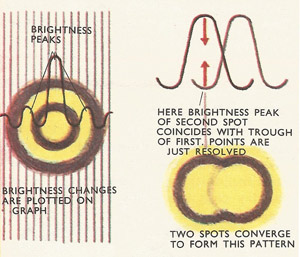
Left, the brightness of the pattern can be plotted on a graph. There is a region of maximum brightness in the central circle followed by minima and maxima in the outer dark and bright rings. Right, according to Rayleigh's criterion the two points are resolved when the central bright maximum of one image coincides with first minimum of the other.
The Rayleigh criterion is a rule for how finely a set of optics may be able to distinguish the location of objects that are near each other; it was proposed by the English physicist Lord Rayleigh. The criterion for resolution is that the central ring in the diffraction pattern of one image should fall on the first dark interval between the Airy disk of the other and its first diffraction ring; for an objective lens of diameter d employing light with a wavelength λ (usually taken to be 5600 Å), the resolution is given approximately by 1.22 × λ/d.
Physical basis of Rayleigh's criterion
It is impossible to design and make a perfect optical instrument. The optical components – lenses and mirrors – invariably have defects and the designer has to bear this in mind and try to create an instrument in which the effect of these is as small as possible. The effects of the most important shortcomings in lenses (chromatic and spherical aberration) have been largely eliminated in more refined pieces of optical equipment. But even when all possible care has been taken in designing an expensive instrument a fundamental defect remains. This results from the wave properties of light itself, and it occurs as a result of diffraction – the break up of light wave fronts that creates interference patterns.
This has an effect on resolving power. For example, if two small bright spots are being observed through a microscope, how far apart must they be before they appear as two separate spots and not as a single blurred image? Assuming that there is no aberration or other optical defect in the system the degree of resolution is finally decided by the diffraction effects in the images of the two spots.
An image is formed because light, which is given out in all directions, is collected by the lenses of the instrument. The lenses make the light converge and bring together all the light that originated from a single object point at a single image point. Suppose the point object is a brightly illuminated tiny spot on a dark background. This is giving out trains of light waves in all directions, each light ray consisting of a series of crests and troughs. Some of the waves will be collected by, say, the central region of the lens, others by the outer regions. The ens brings together all of these rays to form the spot image, the waves passing through all the different parts of the lens must arrive in step – crest reinforcing crest, trough reinforcing rough. Away from the image spot there should be no light at all. Any crests that arrive there should be canceled out by troughs.
This is the theoretical ideal, but it never happens in practice. Not all the light waves that arrive in the image plane outside the central spot are canceled out by other out-of-step waves. Diffraction patterns result with alternate dark and light rings formed outside the central image spot.
The existence of these outer rings spoils the resolution of an instrument. If two object points are viewed through an instrument they will not be resolved if they are too close together. If the separation is increased the image separates into two image points.
It is desirable to be able to say definitely at what separation objects are being resolved by an instrument. Lord Rayleigh suggested an arbitrary criterion for this. In the Rayleigh criterion two points are said to be resolved if the center of the bright central disk coincides with the dark ring around the neighboring image spot. If the image points are closer than this, they are unresolved.


