radial velocity method
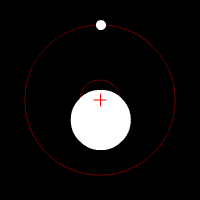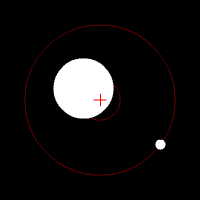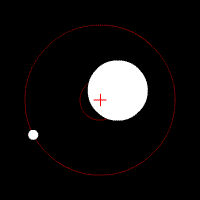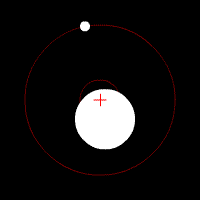
Two bodies with a major difference in mass orbiting around a common barycenter (red cross) with circular orbits.
The radial velocity method is one of the principal techniques used in the search for exoplanets. It is also known as Doppler spectroscopy.
Just as a star causes a planet to move in an orbit around it, so a planet causes its host star to move in a small counter-orbit resulting in a tiny additional, regularly-varying component to the star's motion. Jupiter, for example, causes an additional movement of the Sun with an amplitude of 13 meters per second and a period of 12 years. Earth's effect is much smaller, amounting to fluctuations with a 10 centieters per seconds amplitude over a period of one year. If a star is accompanied by a planet, the radial velocity of the star will periodically change as the star moves toward and then away from a distant observer. If the effect of the planet is sufficiently large, through a combination of its mass and orbital radius, then the back and forth movement of the star is detectable as a small periodic blue shift and red shift in the star's spectral lines. Historically, radial velocity measurements had errors of 1,000 m/s or more, making them useless for the detection of orbiting planets. However, beginning in 1980, Bruce Campbell and Gordon Walker developed a method capable of measuring radial velocities to a precision of 15 meters per second. A number of groups around the world are now using the radial velocity method, with a precision in the range 3 to 10 meters per second in the search for exoplanets.
A drawback of the technique is that, because it measures movement exclusively along the line of sight, it allows only a lower mass limit to be assigned to any invisible companions that it detects. If the orbital plane of the orbiting object happens to lie along our line of sight then the measured speed is the true speed of the wobble. However, if the orbital plane is tilted with respect to the Sun then the true speed is higher and the companion is more massive by a factor of 1/sin i, where i is the angle of inclination. To determine the value of i, and therefore the true mass, radial velocity measurements must be combined with astrometric observations which track the movement of the host star across the sky. Only in this way can researchers check that what might appear to be high mass planets are not actually in the mass range that would suggest they are more likely to be brown dwarfs.


