radius
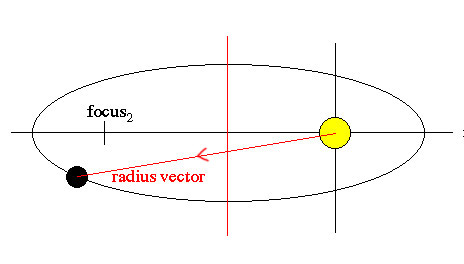
Figure 1. The radius vector of a planet in a highly elliptical orbit around a star.
In mathematics, the radius is the distance from the point of intersection of the axes of symmetry of a closed curve. More specifically, the distance from the center of a circle to its circumference, from the center of a sphere to its surface, or from the center of a regular polygon to any one of its vertices. All radii of a circle or sphere are equal; and it is generally profitable to consider only the longest and shortest radii (semi-major and semi-minor axes) of an ellipse.
Radius vector
The radius vector (Figure 1) is the line joining an orbiting body to its center of motion at any instant, directed radially outward. For a circular orbit, the center of motion coincides with the center of the circle; for a parabolic or hyperbolic orbit, the center of motion is the focus, and for an elliptical orbit it is one of the two foci.
Radius of curvature
The radius of curvature, r, at any point of a curve is r = 1/κ, where κ is the curvature.
In astronomy, a radius is an old instrument for measuring the angular distance between two celestial objects.


