fourth dimension
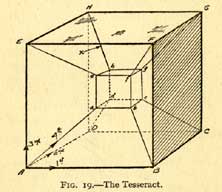
Drawing of a tesseract from "Theosophy and the Fourth Dimension" (1928) by Alexander Horne.
The fourth dimension is an extension at right-angles to the three familiar directions of up-down, forward-backward, and side-to-side. In physics, especially in relativity theory, time is often regarded as the fourth dimension of the spacetime continuum in which we live. But what meaning can be attached to a fourth spatial dimension? The mathematics of the fourth dimension can be approached through a simple extension of either the algebra or the geometry of one, two, and three dimensions.
Algebraically, each point in a multidimensional space can be represented by a unique sequence of real numbers. One-dimensional space is just the number line of real numbers. Two-dimensional space, the plane, corresponds to the set of all ordered pairs (x, y) of real numbers, and three-dimensional space to the set of all ordered triplets (x, y, z). By extrapolation, four-dimensional space corresponds to the set of all ordered quadruplets (x, y, z, w). Linked to this concept is that of quaternions, which can also be viewed as points in the fourth dimension.
Geometric facts about the fourth dimension are just as easy to state. The fourth dimension can be thought of as a direction perpendicular to every direction in three-dimensional space; in other words, it stretches out along an axis, say the w-axis, that is mutually perpendicular to the familiar x-, y-, and z-axes. Analogous to the cube is a hypercube or tesseract, and to the sphere is a 4-d hypersphere. Just as there are five regular polygons, known as the Platonic solids, so there are six four-dimensional regular polytopes. They are: the 4-simplex (constructed from five tetrahedra, with three tetrahedra meeting at an edge); the tesseract (made from eight cubes, meeting three per edge); the 16-cell (made from 16 tetrahedra, meeting four per edge); the 24-cell (made from 24 octahedra, meeting three per edge); the 120-cell (made from 120 dodecahedra, meeting three per edge); and the monstrous 600-cell (made from 600 tetrahedra, meeting five per edge). Geometers have no difficulty in analyzing, describing, and cataloging the properties of all sorts of 4-d figures. The problem starts when we try to visualize the fourth dimension. This is a bit like trying to form a mental picture of a color different from any of those in the known rainbow from red to violet, or a "lost chord," different from any that has ever been played. The best that most of us can hope for is to understand by analogy. For example, just as a sketch of a cube is a 2-d perspective of a real cube, so a real cube can be thought of as a perspective of a tesseract. At a movie, a 2-d picture represents a 3-d world, whereas if you were to watch the action live, in three-dimensions, this would be like a screen projection in four dimensions. See also Klein bottle.
Many books have been written and schemes devised to nudge our imaginations into thinking four-dimensionally. One of the oldest and best is Edwin Abbott's Flatland1 written more than a century ago, around the time that mathematical discussion of higher dimensions was becoming popular. H. G. Wells also dabbled in the fourth dimension, most notably in The Time Machine (1895), but also in The Invisible Man (1897), in which the central character drinks a potion "involving four dimensions," and in "The Plattner Story" (1876), in which the hero of the tale, Gottfried Plattner, is hurled into a four spatial dimension by a school chemistry experiment that goes wrong and comes back with all his internal organs switched around from right to left.2 The most extraordinary and protracted attack on the problem, however, came from Charles Hinton, who believed that, through appropriate mental practice involving a complicated set of colored blocks, a higher reality would reveal itself, "bring[ing] forward a complete system of four-dimensional thought [in] mechanics, science, and art."
Victorian-age spiritualists and mystics also latched on to the idea of the fourth dimension as a home for the spirits of the departed. This would explain, they argued, how ghosts could pass through walls, disappear and reappear at will, and see what was invisible to mere three-dimensional mortals. Some distinguished scientists lent their weight to these spiritualist claims, often after being duped by clever conjuring tricks. One such unfortunate was the astronomer Karl Friedrich Zöllner who wrote about the four-dimensional spirit world in his Transcendental Physics (1881) after attending séances by Henry Slade, the fraudulent American medium.
Art, too, became enraptured with the fourth dimension in the early twentieth century. When Cubist painter and theorist, Albert Gleizes said, "Beyond the three dimensions of Euclid we have added another, the fourth dimension, which is to say, the figuration of space, the measure of the infinite," he united math and art and brought together two major characteristics of the fourth dimension in early Modern Art theory – the geometric orientation as a higher spatial dimension and the metaphorical association with infinity.3
References
1. Abbott. Edwin A. Flatland: A Romance of Many Dimensions.
London: Seely and Co., 1884. Reprinted Mineola, NY: Dover Publications,
1992.
2. Scheick, William J. "The Fourth Dimension in Wells's Novels of the
1920s." Criticism, 20: 167-190, 1978.
3. Henderson, Linda Dalrymple. The Fourth Dimension and Non-Euclidean
Geometry in Modern Art. Princeton, NJ: Princeton University Press,
1983.
4. Banchoff, Thomas F. Beyond the Third Dimension: Geometry, Computer
Graphics, and Higher Dimensions. New York: W. H. Freeman, 1990.
5. Heinlein, Robert. "And He Built a Crooked House," in Isaac Asimov
(ed.) Where Do We Go From Here? New York: Doubleday, 1971.
6. Hendricks, John R. " Images from the Fourth Dimension." Winnipeg,
Canada: self-published pamphlet, 1993.
7. Manning, H. P. Geometry of Four Dimensions. New York: Dover,
1956.
8. Manning, H. P. The Fourth Dimension Simply Explained. New
York: Dover, 1960.
9. Neville, E. H. The Fourth Dimension. Cambridge, England:
Cambridge University Press, 1921.
10. Pickover, Clifford. Surfing Through Hyperspace. New York:
Oxford University Press, 1999.
11. Robbin, Tony. Fourfield: Computers, Art, and the Fourth Dimension.
Boston: Little, Brown, 1992.
12. Rucker, Rudolf v.B. Geometry, Relativity, and the Fourth Dimension.
New York: Dover Publications, 1977.
13. Rucker, Rudy. The Fourth Dimension. Boston: Houghton Mifflin,
1984.
14. Van Cleve, James. "Right, Left, and the Fourth Dimension." The
Philosophical Review, 96: 33-68 (1987).

