hyperbolic geometry
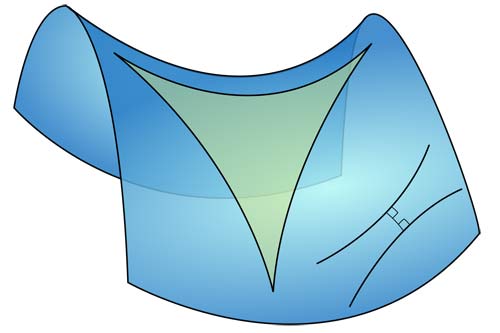
A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), along with two diverging ultra-parallel lines.
Hyperbolic geometry is one of the two main types of non-Euclidean geometry and the first to be discovered. It is concerned with saddle-surfaces, which have negative curvature and on which the geodesics are hyperbolas. In hyperbolic geometry, contrary to the parallel postulate, there exists a line m and a point p not on m such that at least two distinct lines parallel to m pass through p. As a result: the sum of the angles of a triangle is less than 180° and, for a right triangle, the square of the hypotenuse is greater than the sum of the squares of the other two sides.


