elliptical geometry
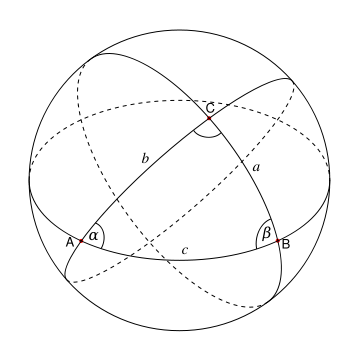
Spherical triangle.
Elliptical geometry is one of the two most important types of non-Euclidean geometry: the other is hyperbolic geometry. In elliptical geometry, Euclid's parallel postulate is broken because no line is parallel to any other line.
Spherical geometry
The original form of elliptical geometry, known as spherical geometry or Riemannian geometry, was pioneered by Bernard Riemann and Ludwig Schläfli and treats lines as great circles on the surface of a sphere. The most familiar example of such circles, which are geodesics (shortest routes) on a spherical surface, are the lines of longitude on Earth. In spherical geometry any two great circles always intersect at exactly two points. Two lines of longitude, for example, meet at the north and south poles. Working in spherical geometry produces some surprising, non-intuitive results. For instance, it turns out that the shortest flying distance from Florida to the Philippine Islands is a path across Alaska – even though the Philippines are at a more southerly latitude than Florida! The reason is that Florida, Alaska, and the Philippines lie on the same great circle and so are collinear in spherical geometry. Another odd property of spherical geometry is that the sum of the angles of a triangle is greater then 180° (see below). This is always the case on a surface that bulges out or, in mathematical parlance, has positive curvature.
Spherical trigonometry
This is the branch of spherical geometry dealing with the ratios between the sides and angles of spherical triangles. The sum of the angles of a spherical triangle is always between 180° and 540°, and the amount by which this sum exceeds 180° for a particular triangle is termed the excess; the area of the triangle is πr 2E/180°, where r is the radius of the sphere and E the triangle's excess. The relations between the sides and angles of a spherical triangle are given by the cosine rule and the sine rule.
Spherical astronomy, of importance in positional astronomy and space exploration, is the application of spherical trigonometry to determinations of stellar positions on the celestial sphere.
Generalization to elliptical geometry
It was Felix Klein who first saw clearly how to rid spherical geometry of its one blemish: the fact that two lines have not one but two common points. He redefined the notion of a point as a set of antipodal points. With this definition, any two points determine a unique line so that the traditional form of Euclid's first postulate is restored. Thus modified, spherical geometry became what Klein called elliptical geometry.


