angle
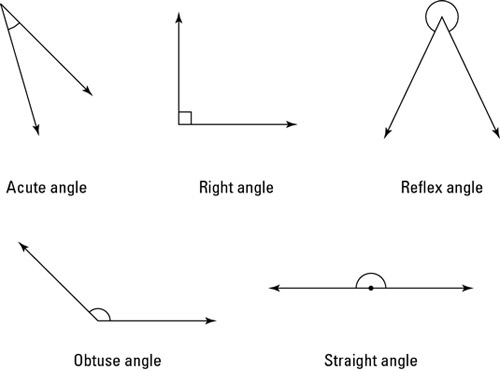
Figure 1. Types of angle.
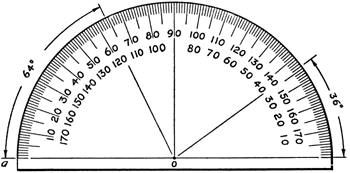
Figure 2. Protractor.

Figure 3. Set square.
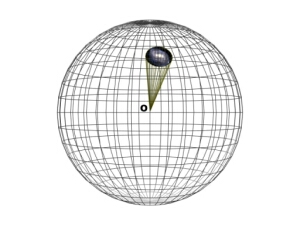
Figure 4. Solid angle.
"My geometry teacher was sometimes acute, and sometimes obtuse, but he was always right." — anonymous
In plane geometry, an angle is the opening between two lines or two planes that meet; the word comes from the Latin angulus for a sharp bend. Plane angles are measured in degrees or radians.
Types of angle
A right angle has exactly 90° (or π/2 radians), an acute angle less than 90°, an obtuse angle has between 90° and 180°, and a straight angle has exactly 180°. Any angle that is at most 180° is said to be convex. An angle between 180° and 360° is called a reflex angle (Figure 1). An angle of exactly 360° is said to be a full angle.
Complementary angles add to give 90°. For example, the angles adjacent to the hypotenuse of a right-angled triangle are complimentary angles (Figure 5).
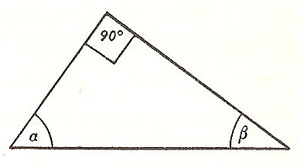 |
| Fig 5. Angles α and β are complimentary.
|
Supplementary angles make a total of 180°. Adjacent angles are next to, and thus share, one side.
Alternate angles are angles on opposite sides and opposite ends of a line that cuts two parallel lines. Opposite angles, occur where parallel lines are cut by a transversal (Figure 6). Opposite angles lie on the same side of the transversal and on different sides of the parallel lines. Angles opposite to the intersecting parallels add up to 180°.
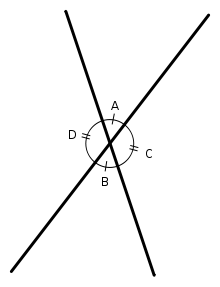 |
| Figure 6. A and B are opposite angles, as are C and D.
|
An external angle, or exterior angle, is an angle between one side of a polygon and the extension of the side adjacent to it. An external angle at any vertex is the supplement of the internal angle there (Figure 7). The sum of the external angles of a convex polygon is always equal to 360° in plane geometry. An interior angle is an angle within a polygon formed by two adjacent sides.
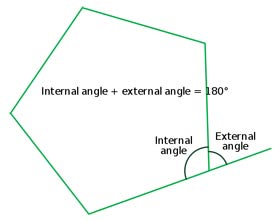 |
| Figure 7. Internal and external angles.
|
A reentrant angle is an inward-pointing angle of a concave polygon.
An inscribed angle is an angle formed by two chords of a curve that meet at the same point on the curve (Figure 8).
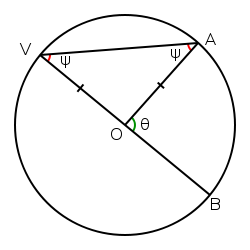 |
| Figure 8. An inscribed angle (BVA) where one chord is a diameter. |
A dihedral angle is the angle defined by two planes or two faces of a polyhedron meeting at an edge; for example, all the dihedral angles of a cube are 90°. An almost-spherical polyhedron (with many faces) has small dihedral angles. A dihedral angle is described by a point on one of the planes or faces, the line of intersection (edge), and a point on the other plane. Should a point P on one of the planes be so positioned that the line through it perpendicular to the edge E, intersects E at the same point as a line drawn perpendicular to E through a point P' on the other plane, then the angle PEP' is the plane angle of the dihedral angle. All plane angles of a dihedral angle are equal.
In spherical geometry, a spherical angle is that formed by intersecting arcs of two great circles; its magnitude is equal to that of the angle between the two planes of the great circles.
Bisecting an angle
Bisecting an angle is a splitting an angle exactly in two using only a pair of compasses and a straightedge. This is easy and the ancient Greeks knew very well how to do it. Put the point of the compass at a point O and draw a circle so that it cuts the two lines coming out from the angle. Call these intersection points A and B. Now put the point of the compass at A and draw an arc that follows within the opening of the angle. Without changing the radius at which the compass is set, move its point to B and draw another arc. Join the point where the two arcs cross, P, to O using the straight edge: angle POB is half of angle AOB
Trisecting an angle
Whereas bisecting an angle could hardly be simpler, splitting an angle in three equal parts with compasses and straightedge alone is impossible, except in a few special cases such as when the angle happens to be 90°. Trisecting an arbitrary angle can be done if you cheat by using a measuring ruler instead of a plain straightedge, or even if you draw just two marks on the straightedge, but not if you play by the rules and the straightedge is completely blank. The Greeks put a huge effort into the problem but couldn't crack it. In fact, the question of whether trisection could ever be done in the general case remained open until 1837, when it was finally shown to be impossible by Pierre Wantzel, a 23-year-old French mathematician. Why is it impossible? Wantzel showed that the two problems of trisecting an angle and of solving a cubic equation are equivalent. Moreover, he showed that only a very few cubic equations can be solved using the straightedge-and-compass method. He thus deduced that most angles cannot be trisected.
Protractor
A protractor (Figure 2) is an instrument for measuring angles. Usually semicircular, it is marked off in degrees along the semicircular edge.
Set square
In classical geometry, a set square (Figure 3) is an instrument used to draw right angles and, with a straight edge particularly, parallel lines. The most basic form of set square is a triangular piece of clear plastic or wood with the center removed and the outer edges beveled. Commonly, the markings of a ruler and a half circle protractor are inscribed. These set squares come in two usual forms, with 90–45–45 degree angles and 30–60–90 degree angles. Combining the two forms by placing the hypotenuses (the longest sides) together yields 15° and 75° angles.
Solid angle
A solid angle is a three-dimensional angle formed by a conical surface (Figure 4). Considering its vertex to lie at the center of a sphere, then a measure of its magnitude may be obtained from the ratio between the area (L2) of the surface of the sphere cut off by the angle, and the square (R 2) of the sphere's radius. Solid angles are measured in steradians (sr), an angle of one steradian subtending an angle of area R 2 at a distance R.

