angular momentum
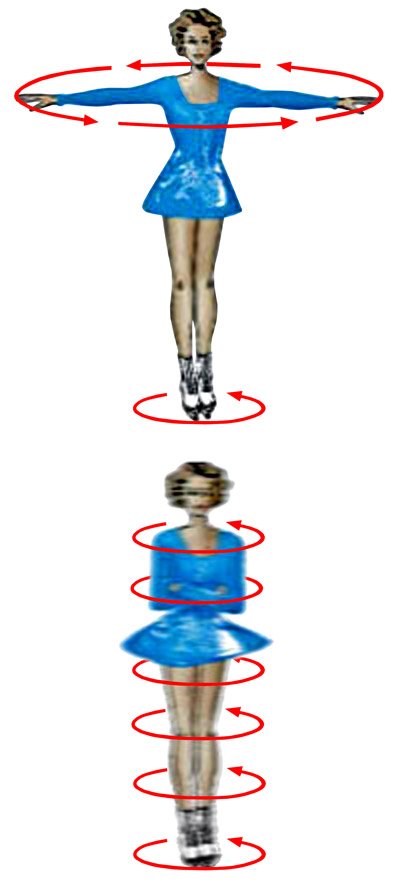
The spin of a skater is slow when the arms are outstretched. Pulling the arms in causes the rate of rotation to increase.
Angular momentum is the momentum that an object or system of objects has because of its rotation. It is a vector quantity directed along the axis of rotation. The angular momentum of a rotating object is equal to the product of the angular velocity (ω) of the object and its moment of inertia (I), i.e., L = Iω. If no external forces act on a rotating system, the direction and magnitude of its angular momentum remain constant; this principle is known the law of conservation of angular momentum.
A spinning skater
A skater starts her spin with arms outstretched. She swings both her arms around to give her body the necessary starting impulse, and slowly she starts her spin. Then, to speed the spin, she pulls her arms tightly to her body. With no extra effort, she spins much faster.
As she twisted her whole body around, the skater gave herself angular momentum. Momentum is a term used to describe the quantity of motion, when the body is moving in a straight line. It is equal to mass multiplied by velocity. Angular momentum is the quantity of spinning motion. It depends, among other things, on the angular velocity of the skater, a measure of the number of spins per second.
The skater's outstretched arms are farthest away from the rest of her body. They are moving quickest through the air. Consequently, they have more angular momentum. The total amount of angular momentum remains the same after the skater has pull in her arms. Angular momentum is one of the quantities in physics which is conserved. Angular momentum with arms outstretched equals angular momentum with arms alongside body.
The sudden increase in the rate of spin comes about when the extra angular momentum of the spinning arms is shared out over her whole body. Angular momentum lost by the arms is gained by the rest of the skater's body, which gains more angular momentum and spins quicker.
Momentum and angular momentum
Momentum equals mass times velocity, but angular momentum does not equal mass times angular velocity. When something is spinning, different parts of it rotate at different velocities. Those parts farthest away from the axis of rotation move the quickest. The quantity that determines the angular momentum and takes into account the distance away from the spinning axis, is called the moment if inertia. Angular momentum is equal to the moment of inertia multiplied by angular velocity.
Orbital angular momentum
Since angular momentum is a conserved quantity in physics, the angular momentum of an orbiting body must stay the same at all points in the orbit. Orbital angular momentum is given by multiplying together a body’s mass (m), its orbital angular velocity (v), and the distance (r) from the body around which it is moving. Since m is constant, v increases as r decreases (and vice versa) in an elliptical orbit. This is why planets in the Solar System, for example, travel faster at perihelion than they do at aphelion. Angular momentum is also conserved for an object spinning on its own axis (like the pirouetting ice skater described above), which explains why stars spin more slowly as they expand and faster as they contract (although any mass loss will carry away some angular momentum).
Angular momentum in quantum mechanics
In quantum mechanics, angular momentum is quantized in units of Planck's constant (divided by 2π). This corresponds classically to only certain frequencies of rotation being allowed. One implication of this is that if electrons are thought of as being in orbit around the central nucleus of an atom. Similarly, the spin of an electron is quantized, and the electron can only exist with spin up (+½) or spin down (-½) measured against some external reference such as a magnetic field.


