bubbles
Figure 1. Bubbles.
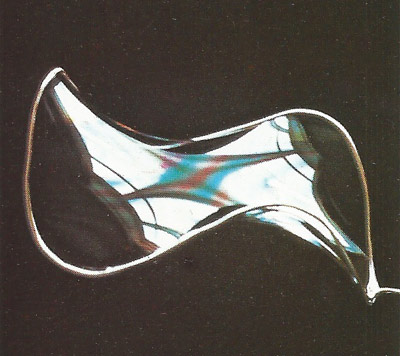
Figure 2. A minimum-area surface formed by a soap film.
Whether alone or in groups joined together, bubbles get their shape by following one simple rule: soap film always tries to form a minimal surface. As a form of amusement for children the blowing of soap-bubbles goes back to ancient times, and is seen depicted on an Etruscan vase in the Louvre. The scientific study of bubbles and films began in earnest in the 1830s with the experiments of Joseph Plateau, who added glycerine to the soap solution to produce bubbles and films that were remarkably durable.
The beautiful play of colors seen on soap bubbles is due to the extreme but variable thinness of their films and is an illustration of the interference phenomenon known as Newton's rings. If at any part the film becomes thin enough a black spot appears. Touching this black spot causes the bubble to break instantly, although in its thicker portions the film can be pierced by a needle without losing continuity.
A single bubble will always try to form a sphere because this shape, as proposed by Archimedes and proved by Hermann Amandus Schwarz (1843–1921) in 1884, is the minimal surface enclosing a single volume. The spherical form is a direct result of the action of surface tension. For a long time, mathematicians believed that the minimal surface for enclosing two separate volumes of air is a double bubble separated by a third surface, which meets the other two along a circle at 120° and is flat if the bubbles enclose the same volume and, otherwise, is a spherical surface that bulges a little into the larger of the two. The double bubble conjecture was finally confirmed by a team of four mathematicians in 2000.
Another great bubble mystery that has recently been solved is why the bubbles in a glass of Guinness appear to sink rather than rise. Bubble's that rise, like those in a saucepan or those breathed out by a diver, are a familiar sight and easy to explain: gas bubbles are lighter than liquid and experience a buoyancy force that drives them up toward the liquid surface. But many of the bubbles in a glass of Guinness can be seen heading downward. Researchers have found that large bubbles in the center of the glass move upward relatively quickly and drag liquid with them. Since the amount of liquid in the glass stays the same (unless someone drinks it!) the liquid moving upward near the center must eventually move back down near the walls of the glass. This downward-moving liquid has a dragging effect on the bubbles. Larger bubbles are more buoyant than smaller bubbles, and continue to move upward. Smaller bubbles (less than 0.05 millimeter in diameter) aren't buoyant enough to resist this drag force, and move downward with the liquid near the sides of the glass. Since Guinness is quite opaque, and these downward-moving small bubbles are close to the side of the glass, it often looks as if almost all the bubbles are moving down.
Shapes of minimum surface area per volume
There is no complete mathematical construction to the general problem (given a closed line) of finding a minimum-area surface that has that line as a boundary. A soap film solves it automatically for any closed line. The film is always in tension and shapes itself to minimize its area. Illustrated here (Figure 2) is one outlining the smooth and elegant minimum-area surface for a three-lobed loop made of copper wire.


