Kaluza-Klein theory
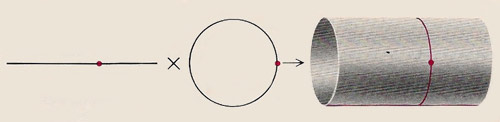
Kaluza's theory regards the fifth dimension as a circle associated with every point in ordinary spacetime. If one dimension of ordinary spacetime is represented as a line, an analog of the five-dimensional structure proposed by Kaluza can be visualized. It is a line to which a circle is associated at every point, or in other words a cylinder. A circular cross section of this cylinder represents the structure of empty, five-dimensional spacetime.
Kaluza-Klein theory is a model that seeks to unite classical gravity and electromagnetism by resorting to higher dimensions. In 1919 the German mathematician Theodor Kaluza (1885–1954) pointed out that if general relativity theory is extended to a five-dimensional spacetime, the equations can be separated out into ordinary four-dimensional gravitation plus an extra set, which is equivalent to Maxwell's equations for the electromagnetic field, plus an extra field known as the dilaton. Thus electromagnetism is explained as a manifestation of curvature in a fourth dimension of physical space, in the same way that gravitation is explained in Einstein's theory as a manifestation of curvature in the first three.
In 1926 the Swedish physicist Oskar Klein (1894–1977) proposed that the reason the extra spatial dimension goes unseen is that it is compact – curled up like a ball with a fantastically small radius. In the 1980s and 1990s, Kaluza-Klein theory experienced a big revival and can now be seen as a precursor of string theory.


