Kepler-Poinsot solids
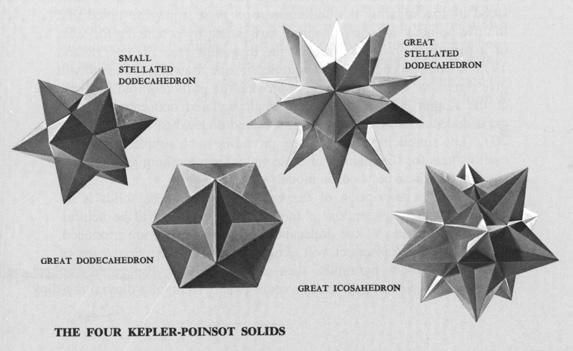
The four Kepler-Poinsot solids. Wenniger, Magnus J. Polyhedron Models for the Classroom. NCTM 1966. p. 11.
The Kepler-Poinsot solids are four regular non-convex polyhedra that exist in addition to the five regular convex polyhedra known as the Platonic solids. As with the Platonic solids, the Kepler-Poinsot solids have identical regular polygons for all their faces, and the same number of faces meet at each vertex. What is new is that we allow for a notion of "going around twice," which results in faces that intersect each other.
In the great stellated dodecahedron and the small stellated dodecahedron, the faces are pentagrams (five-pointed stars). The center of each pentagram is hidden inside the polyhedron. These two polyhedra were described by Johannes Kepler in 1619, and he deserves credit for first understanding them mathematically, though a 16th century drawing by the Nuremberg goldsmith Wentzel Jamnitzer (1508–1585) is very similar to the former and a 15th century mosaic attributed to the Florentine artist Paolo Uccello (1397–1475) illustrates the latter.
The great icosahedron and great dodecahedron were described by Louis Poinsot in 1809, though Jamnitzer made a picture of the great dodecahedron in 1568. In these the faces (20 triangles and 12 pentagons, respectively) which meet at each vertex "go around twice" and intersect each other, in a manner that is the three-dimensional analog to what happens in two-dimensions with a pentagram. Together, the Platonic solids and these Kepler-Poinsot polyhedra form the set of nine regular polyhedra. Augustin Cauchy first proved that no other polyhedra can exist with identical regular faces and identical regular vertices.


