pendulum
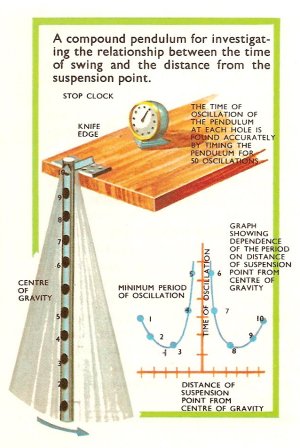
Figure 1. Compound pendulum.
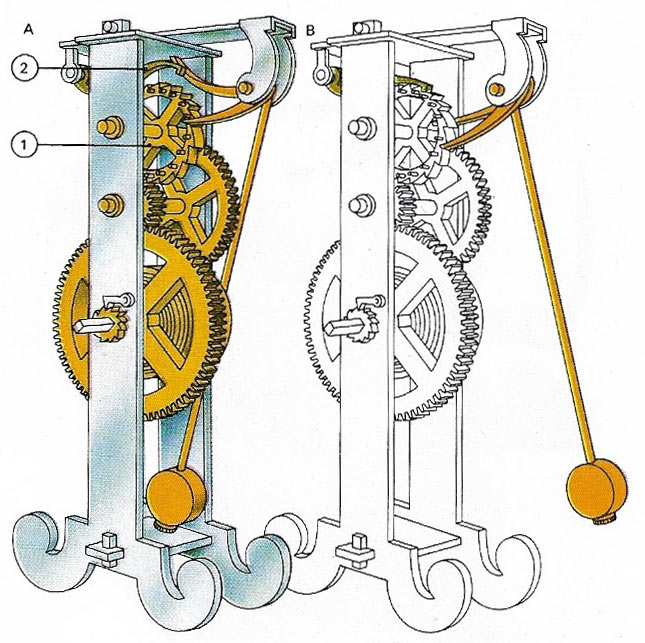
Figure 2. As a device to regulate speed a pendulum operates on the simple principle that the longer the pendulum the longer its period – the time taken for one complete swing from side to side. Galileo applied this principle to regulate the escapement wheel of a clock. His wheel (1) had 12 projecting pins lined up with notches round the circumference. As the pendulum swung inward (A) it lifted a constraining pallet (2) and pushed the pins, allowing the wheel to rotate but only until, with the reversal of the pendulum swing (B), it was once again constrained by the pallet.
A pendulum is any body suspended at a point so that it swings in an arc. A pendulum swinging under gravity marks out equal intervals of time. This fact, supposedly first observed by Galileo in the Cathedral at Pisa, enabled him to design the first pendulum clock. The credit for the general use of pendulums in clocks goes to the Dutch physicist Christiaan Huygens in 1673. There are various types of pendulums.
Simple and compound pendulum
The simple pendulum consists of a weight or bob swinging on the end of a string or wire. In the case of an ideal simple pendulum, when the angle described by the pendulum is small, the string has negligible weight, and the mass of the pendulum is concentrated at one point, the time of one complete swing, T, is given by the formula 2π√(l/g), where l is the length of the string, and g is the acceleration due to gravity.
At a place where g is smaller, such as on the Moon, the period will be longer and pendulum clocks will go slow. The dependence of the period on g is a useful way for checking the surface gravity at different points on the Earth.
To provide the force which tips the escapement wheel in pendulum clocks,a simple pendulum which is without rigidity would be no use so a rigid compound pendulum is the type used.
An easily constructed compound pendulum is a long metal tube with holes bored in it at equal intervals (Figure 1). The pendulum is balanced on a knife edge at these hole. As the point of suspension is moved toward the center of the tube (the center of gravity) the period of oscillation diminishes and then starts to increase again. This means there is a certain distance from the center of gravity at which the period of oscillation is a minimum. If the pendulum is hung the other way up, the same point can be found on the other side. The minimum period of oscillation of the compound pendulum is that same as that of a simple pendulum the length of which is the distance between these two points. The value of g was determined in London in 1817 using this method.
Compensated pendulum
The period of a pendulum depends directly on its length. Any variation in temperature could change the length and alter the period. In clocks this problem is overcome in different ways. Large church clocks often have wooden connecting rods for their pendulums. Wood expands little with heat. Often a compensated pendulum, which depends on the different expansion with heat of different materials is used in clocks. Though the connecting rod may expand with heat and lower, the bob (or its support) expands upward. The net result is that the length of the bob from the pendulum stays the same.
Foucault pendulum
One of the most celebrated historical pendulums is the one invented by Charles Foucault in 1851, to show the rotation of the Earth (see Foucault's pendulum). An iron ball was hung at the end of a 200-foot steel wire. It was then drawn aside and tied with a thread in that position. The thread was burned through and pendulum started swinging slowly. The heavy pendulum maintained its original direction of swing and the Earth rotated beneath it.
One of these pendulums at the North Pole, if it kept swinging, would do a complete revolution in 24 hours; in London it would take 30 hours 40 minutes. At the equator it would not appear to rotate at all. In the northern hemisphere it would rotate clockwise; in the southern hemisphere anticlockwise. In fact the number of degrees it would appear to turn through per hour, at any place on Earth, would be the sine of the angle of latitude multiplied by 15.
Spherical pendulum
A ball swinging around in a circle at the end of a string is called a conical pendulum. A conical pendulum of a certain length has the same period of oscillation as a simple pendulum of the same length. Both of these pendulums are special examples of the spherical pendulum – a ball on a string swinging around in an ellipse. A straight line (the simple pendulum) and a circle (the conical pendulum) are both extreme kinds of ellipse.
One of the interesting motions of this pendulum is barely noticeable. As the ball swings around in ellipses, the ellipses rotate and start to trace out a rosette pattern. The gradual turning around of the ellipses is very slight, compared with the backward and forward oscillatory motion.
Care must be taken in starting a Foucault pendulum because if it is accidentally given the slightest sideways motion it becomes a spherical pendulum and will trace out an elliptical path. The turning around of the ellipses will then mask the rotation die to the Earth. This why it is started by burning a thread with a match so as to make it swing in one plane.
The torsional pendulum is called a pendulum but it does not depend on gravity. It is a heavy body spinning back and forth at the end of a long wire, and can be used in the laboratory to find the resistance to twisting of the material of the wire. A bar swinging from two parallel strings at its ends is called a bifilar pendulum. Its period does not depend on the mass of the bar.


