logic

Symbolic logic.
Logic is the branch of philosophy and mathematics concerned with analyzing the rules that govern correct and incorrect reasoning or inference.
Historical development
The first major exponent of logic was Aristotle, who analyzed terms and propositions and in his Prior Analytics set out systematically the various forms of syllogism; this work has remained an important part of logic ever since. Aristotle's other great achievement was the use of symbols to expose the form of an argument independently of its content. Thus a typical Aristotelian syllogism might be: all A is B; all B is C; therefore all A is C. This formalization of arguments is fundamental to all logic.
Aristotle's pupil Theophrastus developed syllogistic logic, and soma of the Stoics used symbols to represent not single terms but whole propositions, but apart from this there were no significant developments in later antiquity or the early Middle Ages, although logic (dialectic) was part of the trivium. From the 12th century onward there was greater revival of interest in logic: Latin translations of Aristotle's logical works (collectively called the Organun) were studied intently, and a kind of program emerged, which was based on Aristotle and included much that would nowadays be regarded as grammar, epistemology, and linguistic analysis. This Scholastic period was a great age of commentaries and compendiums, with much refinement and minute analysis but little original work. Among the most important medieval logicians were William of Ockham, Albert of Saxony, and Jean Buridan.
After the Renaissance an anti-Aristotelian reaction set in, and logic was given a new turn by Petrus Ramus and by Francis Bacon's prescription that induction (and not deduction) should be the method of the new science. In the work of George Boole and Gottlob Frege the 19th century saw a vast extension in the scope and power of logic. In particular logic became as bound up with mathematics as it was with philosophy. Logicians became interested in whether particular logical systems were either consistent or complete. (A consistent logic is one in which contradictory statements cannot be validly derived.) The climax of 20th-century logic came in the early 1930s when Kurt Gödel demonstrated both the completeness of Frege's first-order logic and that no higher-order logic could be both consistent and complete.
Symbolic logic
Symbolic logic has its roots in earlier logical systems, such as the syllogistic logic created by Aristotle. Yet those earlier systems invariably used words and natural languages to formulate arguments. In contrast, symbolic logic is a formalized language of arguments and reasoning for making and analyzing claims. It is formalized in the sense that it uses different symbols to represent declarative statements, such as "birds are animals", and other symbols to represent operations or functions, such as "and", "or", "if", and "then". Like all of mathematics, it is not dependent upon the user's language.
In the 18th century, German philosopher Gottfried Leibniz made an attempt at creating a symbolic system of logical reasoning. In the 19th century, English mathematician and logician Boole published influential works on mathematical and algebraic logic. Yet German mathematician Frege is widely regarded as the inventor of modern symbolic logic after the publication of Begriffsschrift (Concept Notation) in 1879.
Both mathematics and philosophy are dependent on the use of logic. The dream for many philosophers had long been to create a logical notation system that would quickly reveal the validity or invalidity of an argument simply by looking at it and understanding in symbols, just as mathematicians do when looking at a mathematical equation. With the introduction of symbolic logic, philosophers could delve into the logical structure hidden behind classical arguments, allowing them to solve some of the more troubling philosophical conundrums, such as St. Anselm's ontological argument for the existence of God. More pragmatically, symbolic logic would also become the basis for computer programming.
Well-formed formula
The concept of a "well-formed formula" (WFF) is a key element of modern logic, mathematics, and computer science. The idea of an appropriate and correct rendition of a word in a formal language is first explicitly mentioned in David Hilbert and Wilhelm Ackermann's Grundzuge der Theoretischen Logik (Principles of mathematical Logic) in 1928. A formal language can be thought of as identical to the set of its WFFs, and the words or symbols in formal languages are governed by the rules of the formal language. The set of WFFs may be broadly divided into theorems (statements that have been proven on the basis of previously established statements) and non-theorems. Formal languages are, more specifically, artificial logical languages, governed by a highly regulated set of rules. In the formal language of symbolic logic (the logic of propositions), for example, one basic example of a WFF is called modus ponens and looks like this:
If P, then Q or P → Q
P or P
Therefore, Q or Q
We can fill in the P and Q using philosopher Rene Descartes' well-known dictum: "If I think, then I am. I think. Therefore, I am."
All formal languages must have syntax, concrete definitions of not only the vocabulary must count as WFFs. The concept of a WFF has become well known, for example, in the game WFF 'N PROOF: the Game of Modern Logic designed to teach symbolic logic to children.
Modal logic
Modal logic was devised in 1918 by the American academic philosopher Clarence Lewis (1883–1964), one of the founders of modern philosophical logic, in an attempt to circumvent the paradox of implication – that a false proposition was capable of implying any proposition. It has since developed into a mathematical tool for the study of description languages that discuss various types of relational structures.
Lewis was interested in looking at the reasoning behind everyday modalities (modes of truth), such as "It should be that…," and "It ought to be the case that…," and how their ambiguous phrasing seemed to allow for two kinds of truth, necessary and contingent. Consider the statement, "It is summer." But is it necessarily summer? Is it summer right now, or at some point in the future? Fly to the opposite hemisphere and it certainly old not be summer there. Logicians refer to such modifications to an initial assertion as "modalities" and examine the mode in which the statement could be considered to be true. The truth tables of basic logic cannot easily handle such ambiguities, and so Lewis promulgated "modal logic" to tease apart the contradictions in beliefs, possibilities, and the supposed truth of judgments.
Modal logic's principles are now used in linguistics, artificial intelligence, computer science, and game theory. Modal logic – given impetus by many logicians who have since expanded upon Lewis's original precepts – has come a long way since Lewis first propounded it, as the biannual Advances in Modal Logic conferences attest.
Terms and topics in logic
a priori
The terms a priori and a posteriori are descriptive of knowledge or reasoning, reflecting whether or not it is the result of our experience of the real world. Alleged knowledge attained solely through reasoning from arbitrary principles is a priori (Latin: from earlier things); that gained empirically, from observation or experience, is a posteriori (Latin: from later things). This modern usage of the terms derives from the philosopher Kant.
argument
A mathematical proof, possibly an informal one.
axiom
A statement or proposition that is considered to be true without need of proof. An axiom need not be self-evident but should be consistent with the other axioms of a logical system. The term "axiom" comes from the Greek axios meaning "worthy" and was used by many Greek philosophers and mathematicians, including Aristotle. Curiously, Euclid, whose axioms are best known of all, seems to have favored a more general phrase meaning "common notion."
Closely related is the postulate which is a less arbitrary or basic assumption, provisionally accepted for some particular purpose but more freely open to substitution.
axiomatic method
A method of mathematical reasoning based on logical deduction from assumptions known as axioms. The method is fundamental to the philosophy of mathematics. It was used by the Greeks and formalized in the early twentieth century by David Hilbert. In an axiomatic system, certain undefined entities (terms) are taken and described by a set of axioms. Other, often surprising, relationships (theorems) are then deduced by logical reasoning.
complete
Describes a formal system in which all statements can be proved as being true or false. Most interesting formal systems are not complete, as demonstrated by Gödel's incompleteness theorem.
conjecture
A mathematical statement that has been put forward as a true statement, but that no one has been able yet to prove or disprove; in mathematics, a conjecture and a hypothesis are essentially the same thing. When a conjecture has been proven to be true, it becomes known as a theorem. Famous conjectures include the Riemann hypothesis, the Poincaré conjecture, the Goldbach conjecture, and the twin primes conjecture. Just to show how terminology can be used inconsistently, however, the most famous of all conjectures, for centuries before its proof in 1995, was always known as Fermat's last theorem!
conjunction
The assertion that two statements are both true. For statements a and b, this is written A Λ B, read "a is true and b is true."
consistency
An axiomatic theory is said to be consistent if it's impossible (within the confines of the theory) to prove simultaneously a statement and its negation. Gödel's incompleteness theorem states that any (sufficiently powerful) consistent axiomatic theory is incomplete.
contingency
The property whereby a statement may be either false or true, its truth or falsity depending on the actual state of the world. The statement "the paper in this book is white" is contingent in that although it is in fact true, it is conceivable that it might have been, say, pale green. Compare with necessity.
disjunction
A logical proposition produced by joining two simple propositions by the word "or". An example is the proposition "John is intelligent or John is modest"; it is false if both parts are separately false, otherwise it is true. The disjunction is used in mathematics – in which the proposition is true if either or both components are true. The disjunction of two simple propositions, P or Q, is written P ^ Q, and read "P or Q".
Euler diagram
A simple diagram used in logic to illustrate syllogisms. Classes of objects are represented by circles so that, for example, a premise of the type "some a is b" can be represented by an overlap of two circles, one which represents a and the other representing b. See also Venn diagram.
excluded middle law
A law in (two-valued) logic which states that there is no third alternative to truth or falsehood. In other words, for any statement A, either A or not-A must be true and the other must be false. This law no longer holds in three-valued logic, in which 'undecided' is a valid state, nor does it hold in fuzzy logic.
existence
A term that has several different meanings within mathematics. In the broadest sense there is the question of what it means for certain concepts, such as pi, to exist. Was π, for example, invented or discovered? In other words, does π exist only as an intellectual construct or was it somehow already "out there" waiting for people to find it. If it does exist independently of the human mind, when did its existence start? Does π predate the physical universe?
Such ontological questions become even more difficult when applied to more complex or abstract mathematical concepts such as the Mandelbrot set, surreal numbers, or infinity. A narrower and more technical type of "existence" in math is implied by an existence theorem. Such a theorem is used to prove that a number or other object with particular properties definitely exists, but does not necessarily give a specific example. Finally, there is existence in the sense of particular solutions to problems. If at least one solution can be determined for a given problem, a solution to that problem is said to exist. Something of the flavor of all three types of mathematical existence mentioned here are captured in the following anecdote:
An engineer, a chemist, and a mathematician are staying in three adjoining cabins at an old motel. First the engineer's coffee-maker catches fire. He smells the smoke, wakes up, unplugs the coffee maker, throws it out the window, and goes back to sleep. Later that night the chemist smells smoke too. He wakes up and sees that a cigarette butt has set the trash can on fire. He thinks to himself, "How does one put out a fire? One can reduce the temperature of the fuel below the flash point, isolate the burning material from oxygen, or both. This could be accomplished by applying water." So he picks up the trash can, puts it in the shower stall, turns on the water, and, when the fire is out, goes back to sleep. The mathematician has been watching all this out the window. So later, when he finds that his pipe ashes have set the bed sheet on fire, he's not in the least taken aback. "Aha!" he says, "A solution exists!" and goes back to sleep.
formal system
A mathematical formalism in which statements can be constructed and manipulated with logical rules. Some formal systems, such as Euclidean geometry, are built around a few basic axioms and can be expanded with theorems that can be deduced through proofs.
fuzzy logic
A departure from classical two-valued logic in which something is either true or false, to allow a continuous range of truth values. Fuzzy logic was introduced by Lotfi Zadeh of the University of California at Berkeley in the 1960s as a means to model the uncertainty of natural language.
Gödel's incompleteness theorem
In a nutshell: All consistent axiomatic systems contain undecidable propositions. What does this mean? An axiomatic system consists of some undefined terms, a number of axioms referring to those terms and partially describing their properties, and a rule or rules for deriving new propositions from already existing propositions.
There are a couple of main reasons why axiomatic systems are so useful: first, they're compact descriptions of the whole field of propositions derivable from the axioms, so large bodies of math can be compressed down into a very small compass; second, because they're so abstract, these systems let us derive all, and only, the results that follow from things having the formal properties specified by the axioms. An axiomatic system is said to be consistent if, given the axioms and the derivation rules, it doesn't lead to any contradictory propositions. One of the first modern axiomatic systems was a formalization of simple arithmetic (adding and multiplying whole numbers), achieved the great logician Giuseppe Peano and now known as Peano arithmetic. What Kurt Gödel did was to show that every syntactically correct proposition in Peano arithmetic can be represented by a unique integer, called its Gödel number. (The trick is to replace each symbol in the proposition, including numerals, by a different string of digits. If we represent "1" by 01, "2" by 02, "+" by 10, and "=" by 11, then the Gödel number of "1 + 1 = 2" is 0110011102. Gödel numbers tend to be huge!) This lets us write down, unambiguously, propositions that are about propositions. In particular, we can write down self-referential propositions – ones that include their own Gödel number. From here, Gödel showed that, either the system is inconsistent, or there are true propositions that can't be reached from the axioms by applying the derivation rules. The system is thus incomplete, and the truth of those propositions is undecidable (within that system). Such undecidable propositions are known as Gödel propositions or Gödel sentences. Nobody knows what the Gödel sentences for Peano arithmetic are, though people have their suspicions about Goldbach's conjecture (every even number is the sum of two prime numbers).
So far we've just been talking about Peano arithmetic, but results about an axiomatic system apply to all kinds of things that satisfy the axioms. There are an immense number of other axiomatic systems, which either include Peano numbers among their basic entities or can be constructed from them. (These systems are said to provide models of Peano arithmetic.) It follows that these systems, too, contain undecidable propositions, and are incomplete.
implication
A logical proposition of the type "if P then Q", connecting two simple propositions P (the antecedent) and Q (the consequent). In the form used in mathematical logic the two propositions don't need to be connected. This is called material implication – an example is "if the Earth is flat then gold is a metal". A material implication is false only when the antecedent is true and the consequent false, otherwise it is true.
In normal discourse formal implication is used, in which the simple propositions are related in meaning; for example, "if it does not rain, we will go for a walk."
An implication is written as P → Q, read "P implies Q."
induction
A method of reasoning by which one infers a generalization from a series of instances. Say there is a hypothesis H that contains the variable n, which is a whole number. To prove by induction that H is true for every value of n is a two-step process: (1) prove that H is true for n = 1; (2) prove that H being true for n = k implies that H is true for n = k + 1. This is sufficient because (1) and (2) together imply that H is true for n = 2, which, from (2), then implies H is true for n = 3, which implies H is true for n = 4, and so on. H is called an inductive hypothesis. Some philosophers don't accept this kind of proof, because it may take infinitely many steps to prove something; however, most mathematicians are happy to use it.
necessity
As contrasted with contingency, in logic, the property whereby a statement must be either true or false, this depending on the correct use of language in framing the statement. The statement "this leaf of paper has two sides" is a necessary truth since if it had either more or less than two sides it would not be a leaf according to the normal usage of the term.
necessity and sufficiency
In mathematical analysis, conditions which describe the validity of a statement. For example, in the case of 4 < a < 10 it is necessary that, say, 3 < a < 11 since if this were not true then the original statement would not be true; and sufficient that 5 < a < 9, since is this is true it implies the truth of the original statement. More generally, in logic, a condition is necessary for the truth of a statement if the falsehood of the condition implies the falsehood of the statement, and sufficient if the truth of the condition implies the truth of the statement.
proof
A sequence of statements in which each subsequent statement is derivable from one of the previous statements or from an axiom of a formal system. The final statement of a proof is usually the theorem that one has set out to prove.
Mathematical proof, traditionally, is the logical derivation of claims (theorems) from axioms (claims assumed to be true or taken for granted), and definitions of the terms occurring in the axioms. Although there were mathematicians who proved theorems before him, Euclid is credited as the first to present his proofs in a systematic form. In his seminal work, the Elements (c. 300 BC), theorems are proven on the basis of definitions and axioms. Euclid's use of deductive logic to solve mathematical problems underpinned mathematics for more than 2,000 years.
What is the point of mathematical proof? Axioms and definitions are assumed to have various desirable qualities – to be priori (that is, knowable independently of experience), certain, and necessary – which logical derivation is regarded as preserving. So theorems, when correctly proven, are also a priori, certain, and necessary. Mathematical proof thus enables the mathematician to erect vast structures on the foundations of axioms and definitions, confident that they will topple only if the axioms and definitions are poorly expressed or constructed.
However, controversy about mathematical proof abounds, as three well-known examples illustrate. First, although Euclid thought that one of his axioms of geometry, the Parallel Postulate, was necessary, alternative geometries later rejected it. Second, the philosophy of mathematics called intuitionism holds a different view of what counts as a valid logical derivation and thus of what counts as mathematical proof. Third, in 1976, a computer aided in producing a proof of the four-color theorem in graph theory: because the proof is too lengthy to be checked in its entirety, it is controversial whether it constitutes a proper proof. Still, mathematical proof, as traditionally conceived, continues to be at the center of mathematics.
quantifier
In symbolic logic, the universal quantifier ∀ indicates
"for every" or "for all." For example, ∀ x A, p(x) means for all x belonging to A, the proposition p
quine
Before we put the motion 'that the motion be now put,' should we not first put the motion "that the motion 'that the motion be now put' be now put?" (Chairman of the Meeting of the Society of Logicians) —anonymous
A term named by Douglas Hofstadter after the Harvard logician Willard van Orman Quine. It can be used either as a noun or a verb.
Quine (noun). A computer program that produces an exact copy of itself (or, alternatively, that prints its own listing.) This means that when the program is run, it must duplicate (or print out) precisely those instructions that the programmer wrote as part of the program, including the instructions that do the copying (or printing) and the data used in the copying (or printing.) A respectable quine – one that doesn't cheat – is not allowed to do anything as underhand or trivial as seeking the source file on the disk, opening it, and copying (or printing) its contents. Although writing a quine is not always easy, and in fact may seem impossible, it can always be done in any programming language that is Turing complete, which includes every programming language actually in use.
Quine (verb). To write a sentence fragment a first time, and then to write it a second time, but with quotation marks around it. For example, if we quine "say", we get "say 'say'"). Thus, if we quine "quine", we get "quine 'quine'", so that the sentence "quine 'quine'" is a quine. In this linguistic analogy, the verb "to quine", plays the role of the code, and "quine" in quotation marks plays the role of the data.
reductio ad absurdum
"Reduction to the absurd;" the process of demonstrating that an idea is probably false by first assuming its truth, and then showing how that truth leads to conclusions which can't possibly be true. In A Mathematician's Apology (1941), G. H. Hardy said: "Reductio ad absurdum, which Euclid loved so much, is one of a mathematician's finest weapons. It is a far finer gambit than any chess play: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game."
strange loop
A phenomenon in which, whenever movement is made upward or downward through
the levels of some hierarchial system, the system unexpectedly arrives back
where it started. Douglas Hofstadter has used the strange loop as a paradigm in which to interpret paradoxes
in logic, such as Grelling's paradox and Russell's paradox, and has
called a system in which a strange loop appears a tangled hierarchy.
syllogism
An argument composed of three parts – a major premise, a minor premise, and a conclusion. For example: All men are mortal (major premise). Socrates is a man (minor premise). Therefore, Socrates is mortal (conclusion). The syllogism forms the basis of Aristotle's system of logic, which went unchallenged for over two thousand years. Aristotle believed that by setting out any argument in syllogistic form, it should be possible to avoid fallacies. However, Bertrand Russell discovered several formal errors in the doctrine of syllogism.
theorem
A major mathematical proposition that has been proved correct. More precisely, a statement in a formal system for which there exists a proof; in other words, a statement implied by a set of postulates, or axioms. On the its dependence on the axioms is proved, a newly-discovered theorem becomes a potential stepping-stone to the discovery and proof of other, similarly dependent, theorems.
truth table
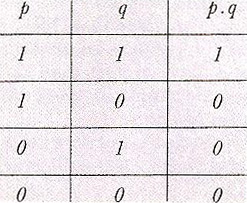 |
In logic, a convenient way of displaying the "truth values" (truth and falsity) of a compound statement as determined by the truth values of its simple component statements. For example, if the simple statements p and q are both true, then the compound statement p and q is true (1); but if either p or q or both p and q are false, then p and q is false (0). This is usually displayed in tabular form as shown.
universe of discourse
The part of the world under discussion; more precisely, the set of all objects presumed or hypothesized to exist for some specific purpose. Objects may be concrete (e.g., a specific carbon atom, Confucius, the Sun) or abstract (e.g., the number 2, the set of all integers, the concept of justice). Objects may be primitive or composite (e.g., a circuit that consists of many subcircuits). Objects may even be fictional (e.g., a unicorn, Sherlock Holmes). The universe of discourse is a familiar concept in logic, linguistics, and mathematics.


