Michelson-Morley experiment
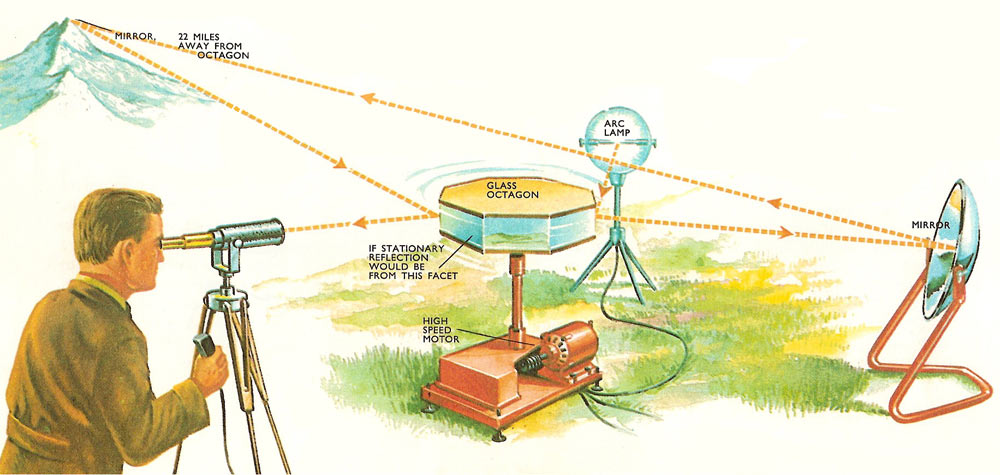
Figure 1. Michelson used a rotating glass octagon to reflect the light. The speed of its rotation was arranged to give a stationary image of the arc lamp.
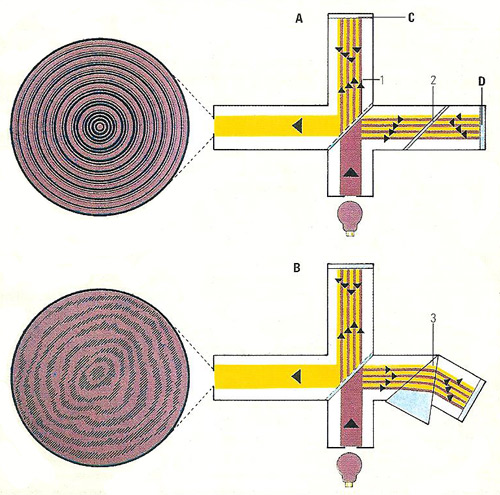
Figure 2. The Michelson interferometer consists of a diagonal mirror (1) which divides the beam from the lamp in half; one half is transmitted to the mirror (C) and the other reflected to the mirror (D). A glass plate (2) is inserted to equalize the path lengths. The beams then return and recombine towards the left where fringes form. An observer sees both the image of C and D. If the planes of these two are parallel, circular fringes appear. Twyman (1918) modified Michelson's interferometer for looking for flaws in glass prisms and lenses (B). The prism to be tested (3) is placed in the light path. If it has imperfections the resulting image will be distorted.
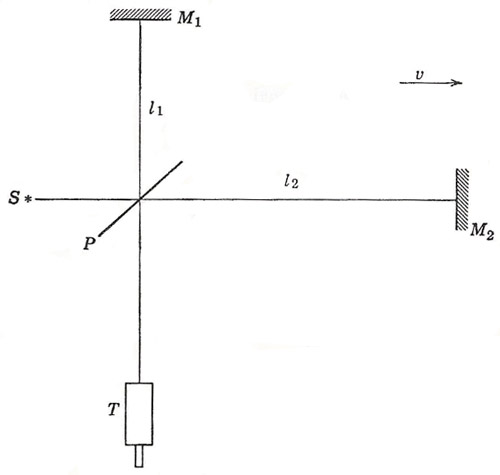
Figure 3. Schematic diagram to illustrate the Michelson_Morley experiment.
The Michelson-Morley experiment was an important experiment whose results, by showing that the ether does not exist, substantially contributed to Einstein's formulation of relativity theory.
Its genesis was the development by Albert Abraham Michelson (1852–1931) of an interferometer (1881) whereby a beam of light could be split into two parts, sent at right angles to each other, and then brought together again. Because of the Earth's motion through space, the "drag" of the stationary ether should produce interference effects when the beams are brought together: his early experiments brought no such effects. With Edward Morley he improved the sensitivity of his equipment, and by 1887 was able to show that there was no "drag," and therefore no ether.
Michelson, awarded the 1908 Nobel Prize in Physics, was the first US Nobel prizewinner.
Theory of the experiment
Suppose that the Earth is moving through a hypothetical ether with speed v in a direction parallel to one limb PM 2 of the interferometer (Figure 3). Then, to make a ray of light go along PM1, we must head it into the "ether wind" so that the resultant of c and v lies along PM1. The resultant velocity of the light in these circumstances is (c 2 — v 2)½. Thus, for the passage of light from P to M, and back, we have
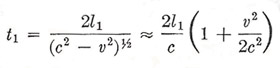 |
For light traveling to M 2 and back, we have simply
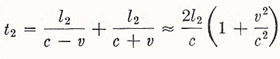 |
Therefore
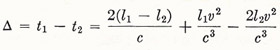 |
Let the apparatus be turned through 90°, thereby interchanging the roles of l1 and l2. We now have
Thus
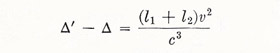 |
The corresponding fringe shift is
In the experiment, the distance l1 + l2 was 22 meters, and λ = 5.9 × 10–5 centimeters. If we take for v the orbital velocity of the Earth (30 km/s), we should then have a fringe shift δ given by
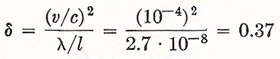 |
Michelson estimated that a shift one hundred times smaller than this should be detectable, though perhaps not measurable, but the result of the experiment was totally negative, although it was repeated at several times of the year. This brought the question of our motion through space to a crucial stage, for it would appear to be an inescapable conclusion that if, by chance, Earth were at rest in space when the experiment was first performed, it could not possibly be again at rest six months later, when the direction of its orbital velocity had been reversed.
Michelson took his null result to mean that Earth dragged some of the surrounding ether along with it, although it was hard to square this idea with the picture of the ether as an all-pervasive, frictionless medium. It became even more difficult to hold to this interpretation after Lodge (1892) measured the speed of light near rapidly rotating bodies, and concluded that not more than 1/200 of the velocity of the bodies was communicated to the ether.
The contraction hypothesis
Experiments with a moving medium by Fizeau (1851) and, as just described, by Michelson and Morley (1885), demonstrated the following:
1. Relative motions of source and observer, or of (source + observer) and material medium, give rise to observable effects.
2. Motion of source, material medium, and observer together relative to a luminiferous ether gives rise to no observable effects.
Now there is an alternative explanation of the null result of the Michelson-Morley experiment (the question of the drag coefficient for moving material media must be put aside for the moment). It was pointed out by Fitzgerald (1892), and independently by Lorentz, that a contraction of bodies along the direction of their motion through the ether would modify the calculations that we have made hitherto. In the arrangement that we have already discussed, we had
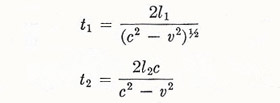 |
If now we suppose that the arm l2 of the apparatus (Figure 3) is shortened l2', such that
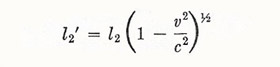 |
we then have
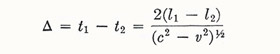 |
and the magnitude of this time difference is completely unaffected by rotation of the apparatus through 90°. A contraction of this sort was obtained by Lorentz in his theory of electromagnetism, which was based on the idea that all physical properties of matter reduce to the properties of electrons. He found that the field equations of electron theory are left unchanged if a contraction by the factor (1 – β2)½ takes place (β = v /c), provided also that a new measure of time is used in a uniformly moving system. (He called this "local time".) At this period the belief that all matter and energy were electrical in origin was becoming prevalent.
The outcome of the Lorentz theory is that an observer perceives the same phenomenon in his system, no matter whether it is at rest in the ether or moving with constant velocity. Different observers are thus equally unable to say whether they are moving or at rest in the ether, so that for optical phenomena,just as for Newtonian mechanics, we have no means of identifying absolute rest. It has become the scientific tradition not to postulate things that are by their nature unobservable, and so it is tempting to suggest that there is no such concept as motion through the ether. This is tantamount to saying that the ether does not exist, but this, nevertheless, was the bold step that Einstein took in 1905 with his special theory of relativity.


