quantum chromodynamics
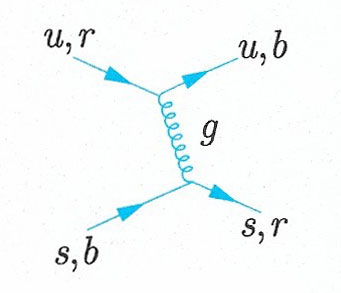
Figure 1. An example of quark-quark scattering by gluon exchange. The gluon is represented by a coiled line to distinguish it from a photon. In this diagram the quark flavir u or s is unchanged on gluon emission, but the color state can change, as shown.
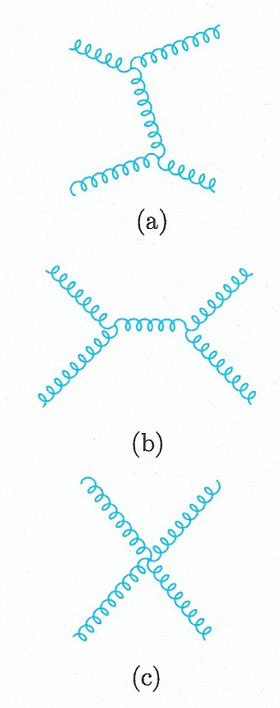
Figure 2. The three lowest-order contributions to gluon-gluon scattering in QCD.
Quantum chromodynamics (QCD) is a quantum field theory that describes the properties of the strong interactions between quarks and between protons and neutrons in the framework of quantum theory and the special theory of relativity.
Although QCD has not been tested to the sameextent or precision as quantum electrodynamics (QED), it is nevertheless in impressive agreement with a large body of experimental data, and is not contradicted by any experiement. QCD is similar to QED in that both describe interactions that are mediated by massless spin-1 bosons coupling to conserved charges. Theories of thos type are called gauge theories because they have a characteristic symmetry known as gauge invariance. Gauge invariance plays a fundamental a fundamental role in theoretical treatments of QED and QCD, where it can be used to infer the detailed forms of the interactions.
Spin-1 bosons are called gauge bosons; in QED they are photons and in QCD they are called gluons and denoted by the symbol g. Gluons have zero electric charge, like photons, but couple to the color charges, rather than to the electric charge. This leads immediately to the so-called flavor independence of strong interactions: that the different quark flavors u, d, s, c, b, and t must have identical strong interactions, because they exist in the same three color states r, g, b, with the same possible values of the color charges. This has its most striking consequences for u and d quarks, which have almost equal masses, where it leads to the phenomenon of isospin symmetry. In the same way, because the mass difference between the s quark and the u and d quarks is small on the scale of hadron masses, it leads to the supermultiplets. Flavor independence also implies the equality of the potentials in the charmonium and bottomium systems.
A second property of strong interactions that follows from the above picture without detailed argument is that the forces between the quarks must be of long range, because the gluons have zero mass. This does not imply that the forces between hadrons are also long range, because hadrons have zero color charges overall. The forces between the "colorless" hadrons are the residues of the forces between their quark constituents, and cancel when the hadrons are far apart.
QED and QCD both describe interactions, albeit of very different strengths, which are mediated by massless spin-1 bosons that couple to conserved charges. However, there crucial difference between them that profoundly affects the character of the resulting forces. It is that while the photons that couple to the electric charge are themselves neutral, gluons have non-zero values of the color charges to which they couple. Figure 1 shows a particular example of a quark–quark interaction by gluon exchange, where the gluon is represented by a "corkscrew" line to distinguish it from a photon. In this diagram, the color states of the two quarks are interchanged, and the gluon has the color quantum numbers
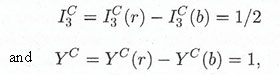 |
which follow from applying color conservation at, for example, the lower vertex, and using the values for the quark color states r and b. Just as quarks exist in three different color states, gluons can exist in eight different color states, and the IC3 and YC values above correspond to just one of them. We do not need to consider these states in detail for what follows, since we shall not attempt any detailed calculations in QCD. Rather, we note that if gluons couple to particles with non-zero color charges, and if gluons themselves also have non-zero charges, then it follows that gluons couple to other gluons. The two types of gluon self-coupling that occur in QCD are shown in Figure 2, which shows the three lowest-order contributions to gluon–gluon scattering. The strength of these interactions is characterized by the strong coupling constant αs, which is analogous to the fine structure constant α in QED. Just as each electron–photon vertex in QED corresponds to a basic process with a transition probability of order α, each quark–gluon vertex and three-gluon vertex in Figs 1 and 2, respectively, corresponds to a basic process of order αs. However, the zero-range "contact" interaction corresponding to the four-gluon vertex in Fig 2(c) is of order αs2, so that all three diagrams in Fig 2 are second-order diagrams, even though Fig 2(c) has only one vertex.
The gluon–gluon interactions of Fig 2 have no analog in QED, and it can be shown that they lead to properties of the strong interaction that differ markedly from those of the electromagnetic interaction. These properties are color confinement and asymptotic freedom. Color confinement is the requirement that observed states have zero color charges. This can be shown to imply that all quark bound states (hadrons) must have integral electric charges. It also implies that gluons, like quarks, cannot be observed as isolated free particles, because they have non-zero values of the color charges. Bound states of two or more gluons with zero color charges overall can be formed in principle, due to the strong interaction between gluons themselves. Such states are called glueballs. Similarly, gluons may bind to, for example, qq̅ pairs, to form colorless states, called hybrids, composed of both quarks and gluons.
Asymptotic freedom means that the interaction gets weaker at short distances, and at distances less than about 0.1femtometer (fm) the lowest order diagrams dominate. At these distances, quark–quark scattering, for example, is given approximately by one-gluon exchange diagrams like Figure 1. However, as the distance between the quarks increases, the interaction gets stronger, and many higher-order diagrams become important. In this strong interaction regime perturbation theory is no longer applicable, and it has not yet been possible to evaluate the theory precisely. We therefore have to rely on approximate results obtained by numerical simulations of the theory on very large computers, and the demonstration of confinement in QCD rests largely on such simulations. They are done using an approach called lattice gauge theory in which space (and sometimes time) is approximated by a finite lattice of discrete points. The exact theory can then in principle be recovered by letting the lattice spac-ing go to zero, and the number of lattice points become infinite. In practice, the number of lattice points that can be handled is limited by the computing power available, but nonetheless good results have been obtained for several static properties, for example the masses and decay constants of the lower-lying hadrons.
The above features are conveniently illustrated by considering the static potential between a heavy quark and its antiquark in a color singlet state. This is the appropriate potential for a non-relativistic discussion of charmonium and bottomonium. Here we are concerned with the behavior predicted on the basis of QCD. At short interquark distances r < 0.1 fm, the interaction is dominated by one-gluon exchange and we might expect a Coulomb-like potential analogous to that arising from one-photon exchange in QED, so that the potential is given by
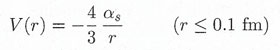 |
where αs is the strong coupling constant discussed above. Because of asymptotic freedom, the strength of the interaction, and hence αs, decreases with decreasing r, but for r < 0.1 fm this variation is slight and can in many applications be neglected. .At distances beyond 0.1 fm, however, the strength of the interaction increases more rapidly and one-gluon exchange no longer dominates. In this region, we have to rely mainly on lattice gauge theory calculations of limited precision. At large distances it can be shown the potential increases approximately linearly
where the constant λ is of order 1 GeV/fm. This is an example of a confining potential in that it does not die away with increasing separation and the force between the quark and antiquark cannot be neglected, even when they are very far apart.
Color charge
Quarks have a distinctive property called color charge which governs their binding together to form other elementary particles. Analogous to electric charge in charged particles, color charge (or, simply, "color") comes in three varieties, arbitrarily known as red, blue, and yellow, and – analogous to positive and negative charges – three anticolor varieties, yellow, magenta and cyan.
Just as positively and negatively charged particles form electrically neutral atoms, colored quarks form particles with no net color. Quarks interact by emitting and absorbing massless particles called gluons, each of which carries a color-anticolor pair. Eight kinds of gluons are required to transmit the strong force between quarks, e.g., a blue quark might interact with a yellow quark by exchanging a blue-antiyellow gluon.
Quarks are not, of course, actually colored – this is just a metaphor for the fact that quarks are always found in groups consisting of all three colors or anticolors (the baryons) or one color and its anticolor (the mesons) or even both (the pentaquark consists of a triplet and a pair). Thus the three colors (or color-anticolor pair) of every particle combine to make white.
The concept of color was proposed by the American physicist Oscar Greenberg and independently by the Japanese physicist Yoichiro Nambu in 1964. The theory was confirmed in 1979 when quarks were shown to emit gluons during studies of high-energy particle collisions at the German national laboratory in Hamburg. QCD is nearly identical in mathematical structure to quantum electrodynamics and to the unified theory of weak and electromagnetic interactions advanced by American physicist Steven Weinberg and Pakistani physicist Abdus Salam (see electroweak force).
Color force
Color force is the force between particles that carry color charge, namely quarks and gluons. This is the force due to the strong interaction. One effect of the color force is to ensure that particles made of quarks (like protons and neutrons) are "white."


