Zeeman effect
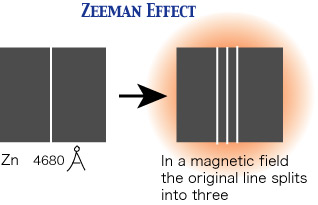
Figure 1. Splitting of the zinc 4680Å line in a magnetic field due to the Zeeman effect.
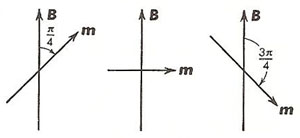
Figure 2. Orientations of the magnetic moment in a triplet excited state due to the Zeeman effect.
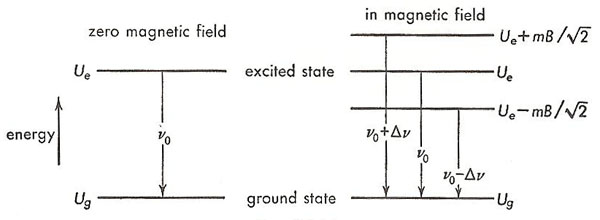
Figure 3. The Zeeman effect, leading to the creation of a triplet, shown as an energy-level diagram.
The Zeeman effect, also known as Zeeman splitting, is the broadening or splitting of a spectral line into several polarized components when the source is in a strong magnetic field. It is named after the Dutch physicist Pieter Zeeman, who shared with Hendrik Lorentz the 1902 Nobel Prize in Physics for the discovery of the phenomenon.
 |
| Pieter Zeeman
|
The Zeeman effect is the magnetic analogue of the Stark effect.
Because the amount of Zeeman splitting and of polarization depend on the magnetic field strength, this effect provides a power tool for investigating cosmic magnetic fields. It was first used to map magnetic fields on the Sun, especially in and around sunspots where the local field strength can be as high as 0.4 tesla – thousands of times stronger than Earth's magnetic field. Across the Sun as a whole, and in the case of most other stars and cosmic objects, the field strengths are much lower and the spectral lines are broadened rather than actually split by the Zeeman effect. However, weak fields can still be studied by measuring the polarization of the line wings – the parts of a spectral line well away from the central peak. Zeeman splitting is observed in the case of some magnetic variables which are associated with intense magnetic fields.
Theory of the Zeeman effect
Most atoms, by virtue of their orbiting electrons, including electron spin, possess net magnetic moments. Such atoms, when placed in a magnetic field, are not allowed to orient themselves arbitrarily with respect to the field. Instead, as predicted by quantum theory, their magnetic moments can only point in certain permitted directions, a restriction known as space quantization. Actually, it is the projection of the magnetic moment in the direction of the field that is quantized. The larger the value of the atom's magnetic moment, the larger the number of orientations permitted to it. Associated with each allowed orientation is a value of potential energy given by the equation
potential energy = – m · B,
where m and B is the magnetic flux density. Thus to whatever internal energy the atom otherwise possesses, the amount – m · B must be added when it is located in a magnetic field.
The emission of an atomic spectral line represents a transition in the atom from a higher to a lower energy state. Since different electronic orbits are involved in the two cases, the magnetic moments of the two states are not necessarily the same. For example, the ground state of a zinc atom has a net magnetic moment that is zero. The 30 orbital electrons belonging to the zinc atom are grouped into 15 pairs, the members of each pair circulating in different orbits but in opposite directions. The orbital magnetic moments and the spin magnetic moments of the 30 electrons neutralize another. In excited states of a zinc atom, however, this complete neutralization seldom occurs. The magnetic moment of certain of the excited states has such a value, say, m, that it is permitted three orientations in a magnetic field, making angles of π/4, π/2, and 3π/4 radians, respectively, with it, as shown in Figure 2.
Consider transitions to the ground state of zinc from one of the excited states that has this value of magnetic moment. These transitions, in the absence of a magnetic field, take place between states of energy Ue and Ug, respectively, as shown in the energy-level diagram on the left of Figure 3. Each transition results in the emission of a photon of light of frequency, ν0, given by
hν0 = Ue – Ug
a relation known as Bohr's second postulate.
When the zinc atoms are placed in a magnetic field, the excited energy level splits into three levels, corresponding to the orientations shown in Figure 2 and having energies Ue – (mB/√2), Ue, and Ue + (mB/√2), respectively, as shown on the right side of Figure 3. The ground state, since it has zero magnetic moment, is not altered by the presence of the magnetic field. The radiation emitted in the transition now consists of three components – the original single spectral line has become a triplet. The middle component has the same frequency, ν0, as the original, but the frequencies of the other two are higher and lower, respectively, than the original and by the same amount,
Δν = m · B/h = mB/√2h
This splitting of a spectral line into three components when the source of light is placed in a magnetic field is known as the normal Zeeman effect. The term anomalous Zeeman effect is applied when the number of components exceeds three. Despite its name, its occurrence is more common than the "normal" behavior.


