Pappus of Alexandria (3rd century AD)
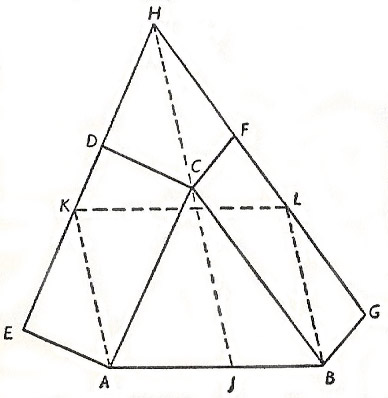
Diagram to illustrate Pappus's theorem.
Pappus of Alexandria was the last of the great Greek geometers whose eight-volume Mathematical Collection summarized the bulk of mathematics known at that time. In this compendium, Pappus added a considerable number of his own explanations and amplifications of the earlier work of Euclid, Archimedes, Apollonius, and others.
The dates when he lived are not accurately known. Suidas states that Pappus was a contemporary of Theon, thus placing him toward the end of the 4th century, and ascribes several treatises to him. These treatises have not survived, and the only work by which Pappus is now known, his Mathematical Collection, receives no mention from Suidas. This work consisted of eight books, the first and the earlier part of the second of which are lost, and its interest is mainly, though not exclusively, historical. From what remains of the second book, it is conjectured that the first two books were arithmetical, The third book explains some of the methods for duplicating the cube, and deals with progressions and the five regular polyhedra. The fourth book discusses the figure called the arbelos, the Archimedean spiral, the conchoid of Nicomedes, and the quadratrix of Hippias. The fifth book contains some theorems regarding isoperimetrical figures, plane and solid, and a short account of Archimedean solids. The sixth book comments on some of the works of Theodosius, Aristarchus of Samos, and Euclid. From the seventh book, which is the longest and most valuable of the Collection, is derived a large part of our knowledge of Greek geometry. Many of the writings here analyzed are no longer extant, and it is on the indications (in the notable instance of Euclid's Porisms, the very obscure indications) which Pappus gives of the object or the contents of them that the geometers of the seventeenth and eighteenth centuries relied for their restorations of these writings. The eighth book is devoted mainly to mechanics.
The mathematical interest of the Collection does not equal the historical, but several of the books contain important theorems, the discovery of some of which may be due to Pappus himself. The last six books of the Mathematical Collections were translated into Latin by Commandinus, an Italian geometer, and were published in 1588; another edition appeared in 1660.
Pappus's theorem
On two sides of a triangle ABC (see diagram) construct arbitrary parallelograms ACDE and BCFG; extend the sides ED and ED and FG to meet in the point H; draw lines through A and B parallel to HC meeting HD and HF in K and L respectively; join KL. We now have a third parallelogram ABLK whose area is equal to the sum of the areas of the two original parallelograms.


