parallax
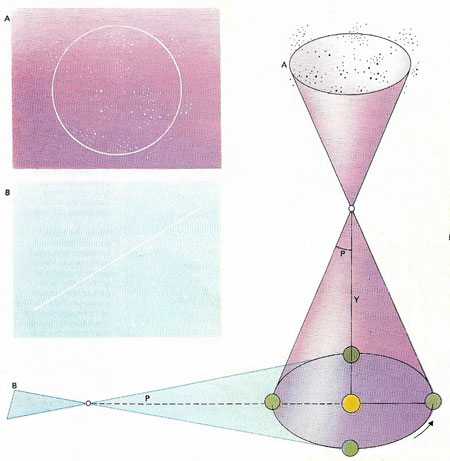
Apparent parallaxes of stars are illustrated in these diagrams. The parallaxes are measured for the apparent movements of relatively nearby stars against a background of more remote stars, which are too distant for any detectable motion. With stars lying in the direction of the axis (Y) of Earth's orbit, the parallactic motion over a year will be circular (A). If a star is co-planar with the elliptic (B), the parallactic motion will take the form of a to-and-fro straight line. P is the angle of a parallax and from this the distance of the star can be measured. The main difficulty is, of course, that the angle P is always very small. With modern photography and other techniques we can now 'see' out to at least 200 light-years, but at greater distances the parallax shifts are swamped by observational errors.
Parallax is the apparent change in position of a relatively close object compared to a more distant background as the location of the observer changes. Annual parallax is the change in the apparent position of a star resulting from Earth's annual motion around the Sun; it is defined as the angle subtended at the object by the semimajor axis of Earth's orbit.
The largest parallax known for an object outside the Solar System is that of the nearest star, Proxima Centauri, 0.762 arcsecond; the first stellar parallax to be measured was that of 61 Cygni. Knowing the parallax p of a star in arcseconds, it is a simple matter to work out the star's distance d in parsecs:
d = 1/p
In the case of Proxima Centauri, d = 1/0.762 = 1.31 parsecs. Multiplying this by 3.26 gives the distance in light-years (4.28 light-years).
There are other ways to measure a stellar distances, which, though not involving trigonometric parallax, are still referred to as varieties of parallax.
Spectroscopic parallax is the most widely used technique for determining the distances of stars that are too distant for their trigonometric parallaxes to be measured. From an analysis of a star's spectrum, its position is determined on the Hertzsprung-Russell diagram, which gives the absolute magnitude. By comparing the star's absolute magnitude with its apparent magnitude, its distance follows directly. Dynamical parallax is a method for determining the distance to a visual binary star. The angular diameter of the orbit of the stars around each other and their apparent brightness are observed. The distance comes from an application of Kepler's laws of planetary motion and the mass-luminosity relation.
The mean parallax is the distance, derived by means of statistical studies of brightnesses and motions, for a group of stars whose individual distances are unmeasurable.
Parallactic displacement
Parallactic displacement is the apparent change in a star's position caused by the movement of Earth in its orbit; also known as parallactic motion. Over the course of a year, a star appears to follow a small path in the sky called a parallactic ellipse, or a parallactic orbit, the shape of which ranges from a circle for a star at the ecliptic pole to a line for a star on the ecliptic.
Solar parallax
Solar parallax is the angle subtended by Earth's equatorial radius at the center of the Sun at the mean distance between Earth and the Sun (1 astronomical unit); equal to 8.794 arcseconds.


