magnitude
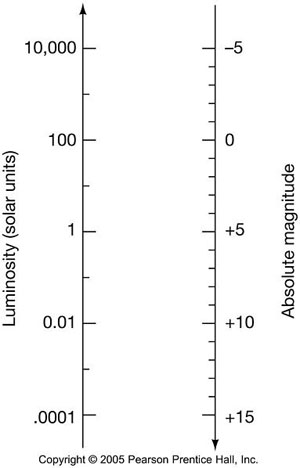
Figure 1. Luminosity and absolute magnitude scales compared. Image used with permission.
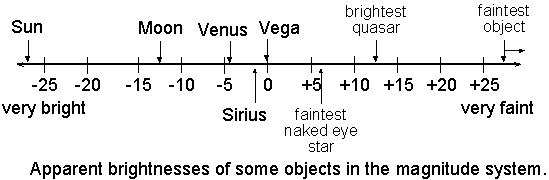
Figure 2. The apparent magnitudes of some astronomical objects.
The magnitude is the brightness of a celestial object, measured on a scale in which lower numbers mean greater brightness. The magnitude system stems from the ancient Greeks and, in particular, Hipparchus who, in about 120 BC, ranked stars from first to sixth magnitude: those of first magnitude being the first to appear after sunset, those of sixth magnitude being at the limit of naked-eye visibility in a dark sky. In the 19th century, when the advent of photometers made it possible to measure accurately the relative brightness of stars, the system was put on a strict quantitative footing by the English astronomer Norman Pogson (1829–1891). In 1856, the magnitude scale was fixed so that a difference of 5 magnitudes corresponded to a ratio of apparent brightness of 100. On this new scale, known as the Pogson scale, defined so that most of the traditional magnitudes of stars stayed roughly the same, a difference of one magnitude corresponds to a change in brightness by a factor of 2.512, while a jump of 5 magnitudes equals a brightness change of exactly 100-fold.
Absolute magnitude
Absolute magnitude, like luminosity, is a measure of the true brightness, or radiative power output, of an object in space. It is based on a logarithmic scale (Figure 1). Absolute magnitude M is the apparent magnitude of a star, or other luminous object, when seen from a standard distance of 10 parsecs (32.6 light-years). It can be found from the object's apparent magnitude m and its parallax π in arcseconds using the formula
M = m + 5 + 5 logπ
The Sun, for example, has an absolute magnitude of 4.8, while Aldebaran, the brightest star in the constellation Taurus, has an absolute magnitude of -0.63, which is equivalent to saying that Aldebaran is about 350 times more luminous than the Sun.
In the case of an asteroid or comet, the absolute magnitude is the apparent magnitude the object would have at zero phase angle and at a distance of 1 AU (astronomical unit) from both the Sun and the Earth.
See also distance modulus.
Apparent magnitude
Apparent magnitude is a measure of the observed brightness of a celestial object. Apparent magnitude depends on an object’s actual (intrinsic) brightness, its distance from the observer, and, in the case of objects outside the Solar System, the amount of absorption by intervening matter. The brighter an object appears, the smaller the numerical value of its apparent magnitude. A star that is one magnitude brighter than another (e.g., +1 versus +2) looks 2.5 times brighter.
Among the brightest objects in the sky are the Sun (apparent magnitude -26.7), the full Moon (-12.6), Venus (at brightest, –4.7), Sirius (–1.44), Canopus (–0.62), Alpha Centauri (–0.27), and Arcturus (–0.05). On a clear, dark night, the unaided eye can see stars as faint as apparent magnitude +6 (Figure 2).
Unless otherwise qualified, the term is normally taken to mean apparent visual magnitude.
Integrated magnitude is the apparent magnitude that an extended object, such as a nebula or galaxy, would have if all its light were concentrated at a starlike point.
The magnitude of the tenth brightest member is a way of gauging the approximate distance to a cluster of galaxies that involves measuring the apparent magnitude of the cluster's tenth brightest member. The method is based on statistical studies, which show that clusters of galaxies tend to contain similar distributions of brighter and dimmer members. By assuming that the tenth brightest member of every cluster has the same brightness, and taking a standard value for the intrinsic brightness of this galaxy, the distance can be found.
Bolometric magnitude
The bolometric magnitude is the magnitude of a star measured across all wavelengths, so that it takes into account the total amount of energy radiated. If a star is a strong infrared or ultraviolet emitter, its bolometric magnitude will differ greatly from its visual magnitude. The absolute bolometric magnitude absolute of a star is a measure of its total energy emission per second, or luminosity. The bolometric correction is the visual magnitude of an object minus its bolometric magnitude.
Combined magnitude
Combined magnitude is the total brightest of two or more celestial objects, such as the stars of a binary system that appear as a single point to the naked eye. Unfortunately, this can't be found simply by adding the separate magnitudes, m1 and m2, because the magnitude scale is logarithmic. Instead the combined magnitude, m, has to be calculated from the formula:
m = m1 – 2.5 log {1 + antilog [–0.4 (m2 – m1)]}.
Photographic magnitude
Photographic magnitude is the magnitude of a celestial object as measured on a photographic emulsion – a method of measuring apparent brightness that is now obsolete. Because emulsions are especially sensitive in the blue region of the spectrum, a blue star records as being brighter than a red star of the same apparent visual magnitude.
UBV system
The UBV system is a system of stellar magnitudes, devised by Harold Johnson (1921–1980) and William Morgan at Yerkes Observatory, which consists of measuring an object's apparent magnitude through three color filters: the ultraviolet (U) at 3600 Å; the blue (B) at 4200 Å; and the visual (V) in the green-yellow spectral region at 5400 Å. It is defined so that, for A0 stars, B - V = U - B = 0; it is negative for hotter stars and positive for cooler stars. The Stebbins-Whitford-Kron six-color system (U, V, B, G, R, I) is defined so that B + G + R = 0. The difference, B - V is a good measure of a star's actual color. For example, Betelgeuse has B – V = 1.85, indicating that it is quite red. On the other hand, Rigel has B – V = –0.03, indicating that it is bluish. Most stars fall between these extremes, except for a few redder-than-red stars (mostly carbon stars) and a few bluer-than-blue stars (mostly young, high-mass stars).
V magnitude
V magnitude is the apparent magnitude of a star, determined by photometry, in a standard wavelength band in the yellow-green region chosen to correspond with that to which the human eye is most sensitive. In the widely-used Johnson photometry system, the filter used to measure V magnitude has a central wavelength of 5450 Å and a bandwidth of 880 Å.
Visual magnitude
Visual magnitude is the apparent magnitude of a celestial body in a wavelength range approximating that of the human eye. This is usually different from photographic magnitude because photographic emulsions do not exactly match the way the human eye's sensitivity varies with wavelength. Visual magnitude is now essentially synonymous with V magnitude, which is determined photometrically.


