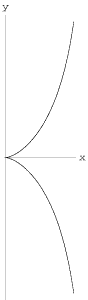
PLANE CURVES A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z                    HOME ABOUT CATEGORIES SITE MAP COPYRIGHT ADVERTISE CONTACT entire Web this site cissoid A plane curve consisting of two infinite branches symmetrically placed with reference to the diameter of a circle, so that at one of its extremities they form a cusp, while the tangent to the circle at the other extremity is their common asymptote. Given a fixed point A and two curves C and D, the cissoid of the two curves with respect to A is constructed as follows: pick a point P on C, and draw a line l through P and A. This cuts D at Q. Let R be the point on l such that AP = QR. The locus of R as P moves on C is the cissoid. The name "cissoid," which means "ivy-shaped," first appears in the work of Geminus in the first century BC. A special case of this curve, now known as the cissoid of Diocles, was first explored by Diocles in his attempt to the solve the classical problem of duplicating the cube. Later investigators of the same curve include Pierre de Fermat, Christiaan Huygens, John Wallis, and Isaac Newton. Newton first showed how to describe the curve by continuous motion. The cissoid of Diocles is traced out by the vertex of a parabola as it rolls, without slipping, on a second parabola of the same size. It has the Cartesian equation y2 = x3/2(a - x). The area include between the two branches of a cissoid and the asymptote is exactly equal to three times the area of the generating circle. Interestingly, Diocles investigated the properties of the focal point of a parabola in On Burning Mirrors (a similar title appears in the works of Archimedes). The problem, then as now, is to find a mirror surface such that when it is placed facing the Sun, it focuses the maximum amount of heat. Related category    • PLANE CURVES Also on this site: Encyclopedia of Alternative Energy & Sustainable Living Encyclopedia of History Transport Concepts & Designs (partner site) BACK TO TOP