thermodynamics
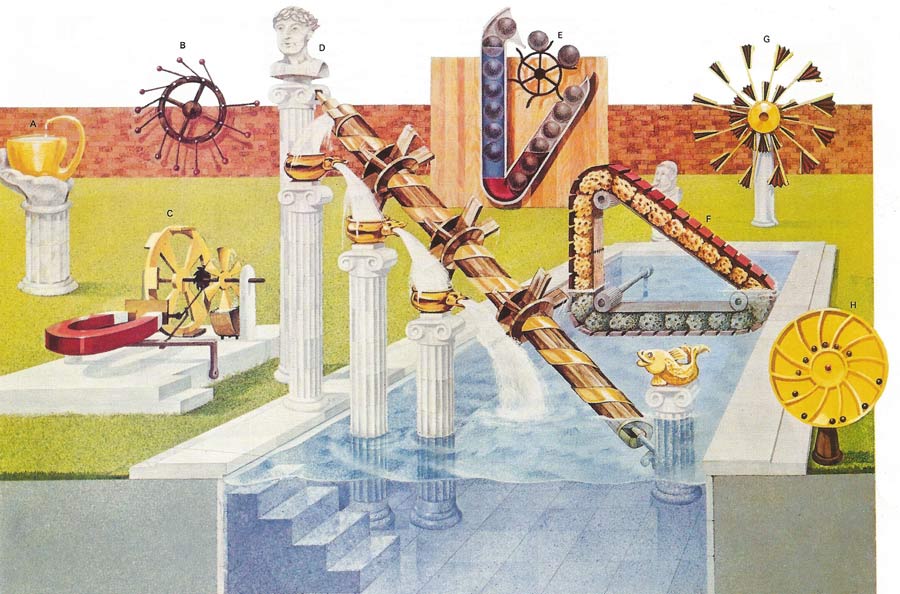
Perpetual motion machines can be classified according to which of the laws of thermodynamics they attempt to violate. The continual operation of a machine that creates its own energy and thus violates the first law would be called a perpetual motion machine of the first kind. There is nothing in the first law to preclude turning the heat of the ocean completely into work and hence drive a cargo ship across the ocean. The second law insists that some of the heat utilized be given up to a heat reservoir at a lower temperature. Thus the temperature difference between the top and bottom of the ocean could be used to do work providing some heat is given up to the colder sea water. If not then the second law is violated, and this machine would be an example of perpetual motion of the second kind. The machines illustrated here are nearly all stopped by friction and not by the laws of thermodynamics. Some may apparently work in defiance of the laws but on closer inspection an unexpected source of energy can be found. Device A uses capillary action to overcome gravity but would exchange heat with the atmosphere in the process. The validity of the laws of thermodynamics had been demonstrated by countless indirect scientific experiments, and no perpetual motion machines have been produced that contravene them. A device could conceivable exist that might be kept in motion without violating these two laws, with only dissipative forces such as friction to slow it down. If the device could be made frictionless then its continual motion would be termed perpetual motion of the third kind. Machines B to H all attempt to gain something for nothing using an apparently greater leverage on one side of a device to turn it. The reasoning behind these attempts to break the first law is faulty and they would remain stationary even without friction. Machines C, D, E, and F had the added dissipative forces of water viscosity or magnetic eddy currents to overcome. Historically thermodynamics was devised for machines containing millions of molecules. Yet single protein molecular machines obey the same laws.
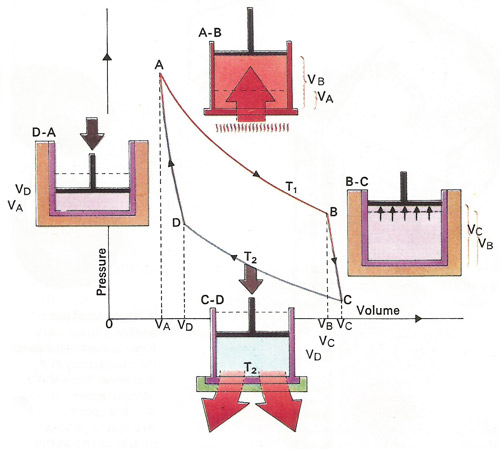
Heat can be converted to mechanical work by allowing a heated gas to expand. Maximum efficiency comes from the Carnot cycle of alternate adiabatic [BC,DA] and isothermal [AB,CD] processes. The former take place without gaining or losing heat, the latter without changing temperature. From A to C the gas raises the piston and preforms work equal to the area below the curve, that is VAABCVC. From C to A it uses work equal to area VAADCVC. The net work obtained equals area ABCD.
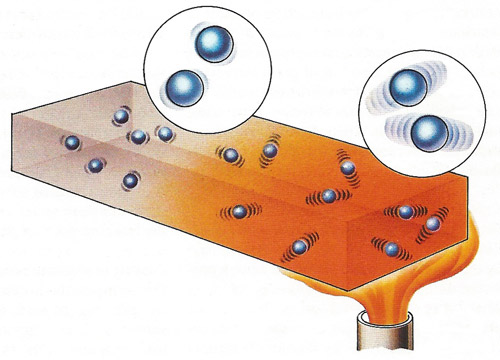
A flame applied to one end of a metal bar transfers heat energy to the atoms of the metal. This raises their kinetic energy so that the atoms begin to vibrate much more vigorously about their fixed mean positions within the lattice network of the metal. As the extent of vibration increases, collisions with neighboring atoms occur so that energy is transferred to these atoms causing them to vibrate. Heat energy is eventually transmitted to the other end of the bar and if the flame is kept in position for some time the temperature at each end of the bar will tend to equalize.
Thermodynamics (meaning "the movement of heat") is a division of physics concerned with the ways in which heat energy travels from one place to another and how heat is converted into other forms of energy. In a heat-transfer process temperature, pressure and volume may each or all undergo various changes. Much of thermodynamics consists of ways of mathematically manipulating these and other parameters to be able to make predictions about the ways in which they will and do change.
Being concerned only with bulk matter and energy, classical thermodynamics is independent of theories of their microscopic nature; its axioms are sturdily empirical, and from them theorems are derived with mathematical rigor. Classical thermodynamics is basic to engineering, parts of geology, metallurgy, and physical chemistry.
Building on earlier studies of the thermodynamic functions temperature and heat, Sadi Carnot pioneered the science by his investigations of the cyclic heat engine in 1824, and in 1850 Clausius stated the first two laws. Thermodynamics was first developed by Joshua Gibbs, Hermann von Helmholtz, William Thomson (Lord Kelvin), and James Clerk Maxwell.
In thermodynamics, a system is any defined collection of matter: a closed system is one that cannot exchange matter with its surroundings; an isolated system can exchange neither matter nor energy. The state of a system is specified by determining all its properties such as pressure, volume, etc. A system in stable equilibrium is said to be in an equilibrium state, and has an equation of state (e.g., the general gas law) relating its properties. (See also phase equilibria.) A process is a change from one state A to another B, the path being specified by all the intermediate states. A state function is a property or function of properties which depends only on the state and not on the path by which the state was reached; a differential dX of a function X (not necessarily a state function) is termed a perfect differential if it can be integrated between two states to give a value XAB (= integral from A to B of dX) which is independent of the path from A to B. If this holds for all A and B, X must be a state function.
Laws of thermodynamics
Historically scientists first derived three laws called the first, second and third laws of thermodynamics, each having different formulations. Then an even more fundamental law was recognized. It has been labelled the "zeroth" law of thermodynamics.
If a hot and a cold object are brought into contact, they finally reach the same temperature. The hot object emits more heat energy than it receives and the cold object has a net absorption of heat. Both objects absorb and emit energy continually, although in unequal quantities, and the exchange process continues until the temperatures equalize. Each object is then absorbing and emitting equal amounts of heat and the objects are said to be in "thermal equilibrium". The zeroth law states that, if two objects are each in thermal equilibrium with a third object, then they are in thermal equilibrium with each other. This underlies the concept of temperature.
The first law states that for any process the difference of the heat Q supplied to the system and the work W done by the system equals the change in the internal energy U: ΔU = Q - W. U is a state function, though neither Q nor W separately is. Corollaries of the first law include the law of conservation of energy, Hess' law (see thermochemistry), and the impossibility of perpetual motion machines of the first kind. For more, see first law of thermodynamics.
The second law (in Clausius' formulation) states that heat cannot be transferred from a colder to a hotter body without some other effect, i.e., without work being done. Corollaries include the impossibility of converting heat entirely into work without some other effect, and the impossibility of perpetual motion machines of the second kind. It can be shown that there is a state function entropy, S, defined by ΔS = ∫dQ/T, where T is the absolute temperature. The entropy change ΔS in an isolated system is zero for a reversible process and positive for all irreversible processes. Thus entropy tends to a maximum. It also follows that a heat engine is most efficient when it works in a reversible Carnot cycle between two temperatures T1 (the heat source) and T2 (the heat sink), the efficiency being (T1 – T2)/T2. For more, see second law of thermodynamics.
The third law states that the entropy of any finite system in an equilibrium state tends to a finite value (defined to be zero) as the temperature of the system tends to absolute zero. The equivalent Nernst heat theorem states that the energy change for any reversible isothermal process tends to zero as the temperature tends to zero. Hence absolute entropies can be calculated from specific heat data. Other thermodynamic functions, useful for calculating equilibrium conditions under various constraints, are: enthalpy (or heat content) H = U + pV; the Helmholtz free energy A = U – TS; and the Gibbs free energy G = H – TS. The free energy represents the capacity of the system to perform useful work. For more, see third law of thermodynamics.
Cooling substances
The third law of thermodynamics states that it is impossible to cool any substance to absolute zero. This zero of temperature would occur for example in a gas whose pressure was zero. All its molecules would have stopped moving and possess zero energy, so that extracting further energy and achieving corresponding cooling would be impossible. A substance becomes progressively more difficult to cool as its temperature approaches absolute zero (–273.16°C)
From the statement of the second law, a heat transfer process naturally proceeds "downhill" - from a hotter to a cooler object. There must be some property or parameter of the system that is a measure of its internal state (its order or disorder), and which has different values at the start and the end of a possible process (one allowed by the first law). This parameter is termed "entropy", and the second law maintains that the entropy of an isolated system can only remain constant or increase.
Careful observation of machines shows that they consume more energy than they convert to useful work. Even if no energy is wasted in friction or lost by necessity, as in a radiator, the available mechanical energy is less than that supplied by the heat source. The entropy of the system is a reflection of its inaccessible energy, and the second law says that it cannot decrease. Heat is a random motion of atoms and when the energy is degraded towards the inaccessible energy pool, these atoms assume a more disorderly state - and entropy is a measure of this disorder.
Under the constraints imposed by the laws of thermodynamics it is possible for a system to undergo a series of changes of its state (in terms of pressure, volume and temperature). In some cases the series ends with a return to the initial state, useful work having been done during the series.
Heat cycles and efficiency
The sequence of changes of the system is called a heat cycle and the theoretical maximum efficiency for such a "heat engine" would be obtained from following the so-called Carnot cycle which is named after the Frenchman Nicholas Carnot (1796–1832). If it were possible to construct a machine operating in cycles, would generate more energy in the form of work than was supplied to it in the form of work than the dream of the perpetual motion machine would be possible. The first law states the impossibility of achieving this result and the second law denies the possibility of even merely converting all the heat to an exactly equivalent amount of mechanical work.
Quantum statistical thermodynamics
Quantum statistical thermodynamics, based on quantum mechanics, arose in the 20th century. It treats a system as an assembly of particles in quantum states. The entropy is given by S = k log P, where k is the Boltzmann constant and P the statistical probability of the state of the system. Thus entropy is a measure of the disorder of the system.


